题目内容
下列函数中既是奇函数,又在区间(0,+∞)上单调递减的函数是( )
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:函数的性质及应用
分析:B和D由复合函数的单调性知,在区间(0,+∞)上是增函数;
A和C在区间(0,+∞)上是减函数,但A不是奇函数,由奇函数的定义知C是奇函数.
A和C在区间(0,+∞)上是减函数,但A不是奇函数,由奇函数的定义知C是奇函数.
解答:
解:A:f(x)=
+
,则f(-x)=
+
=
+
≠-f(x),∴不是奇函数,A不合意意;
B:y=
-
在(0,+∞)上单调递增,B不合意意;
C:f(x)=
+
=
,f(-x)=
=
=-
=-f(x),
∴f(x)为奇函数,又f(x)在(0,+∞)上单调递减,∴C符合题意.
D:y=
-
在(0,+∞)上单调递增,D不合意意;
故选:C.
| 1 |
| 2 |
| 1 |
| 2x+1 |
| 1 |
| 2 |
| 1 |
| 2-x+1 |
| 1 |
| 2 |
| 2x |
| 1+2x |
B:y=
| 1 |
| 2 |
| 1 |
| 2x+1 |
C:f(x)=
| 1 |
| 2 |
| 1 |
| 2x-1 |
| 2x+1 |
| 2(2x-1) |
| 2-x+1 |
| 2(2-x-1) |
| 1+2x |
| 2(1-2x) |
| 2x+1 |
| 2(2x-1) |
∴f(x)为奇函数,又f(x)在(0,+∞)上单调递减,∴C符合题意.
D:y=
| 1 |
| 2 |
| 1 |
| 2x-1 |
故选:C.
点评:本题考查了函数的单调性和奇偶性,运用复合函数的性质判断函数的单调性,运用定义法判断函数的奇偶性,属于基础题.

练习册系列答案
相关题目
抛物线C1:y=ax2(a>0)的焦点与双曲线C2:
-y2=1的右焦点的连线交C1于第一象限的点M,若C1在点M处的切线平行于C2的一条渐近线,则a=( )
| x2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,内角A,B,C的对边分别为a,b,c,若sin2B-sin2C=
sinCsinA,a=2
c,则B=( )
| 3 |
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
复数z=i(i+1),在复平面内,与复数z对应的点Z所在的象限是( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 某同学在电脑上打下了一串黑白圆,如图所示,按这种规律往下排,那么第36个圆的颜色应是( )
某同学在电脑上打下了一串黑白圆,如图所示,按这种规律往下排,那么第36个圆的颜色应是( )| A、黑色 | B、白色 |
| C、白色可能性大 | D、黑色可能性大 |
已知集合A={-2,-1,1,2},B={x|x2-x-2≥0},则A∩(∁RB)=( )
| A、{1} |
| B、{-1,1} |
| C、{-2,1,2} |
| D、{-2,-1,1} |
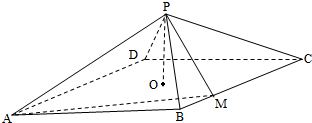 如图,四棱锥P-ABCD,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=
如图,四棱锥P-ABCD,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=