题目内容
l1,l2过p(-
,0)且互相垂直,l1,l2与双曲线y2-x2=1交于A1,B1及A2,B2
①求l1斜率的取值范围;
②若A1为双曲线的一个顶点,求|A2B2|的值.
| 2 |
①求l1斜率的取值范围;
②若A1为双曲线的一个顶点,求|A2B2|的值.
考点:双曲线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:①显然l1、l2斜率都存在,设l1的斜率为k1,得到l1、l2的方程,将直线方程与双曲线方程联立方程组,消去y得到关于x的二次方程,再结合根的判别即可求得斜率k1的取值范围;
②利用①中得到的关于x的二次方程,结合根与系数的关系,利用弦长公式求|A2B2|的值.
②利用①中得到的关于x的二次方程,结合根与系数的关系,利用弦长公式求|A2B2|的值.
解答:
解:①显然l1、l2斜率都存在,否则l1、l2与曲线不相交.设l1的斜率为k1,则l1的方程为y=k1(x+
).
联立得y=k1(x+
),y2-x2=1,
消去y得(k12-1)x2+2
k12x+2k12-1=0.①
根据题意得k12-1≠0,②
△1>0,即有12k12-4>0.③
完全类似地有
-1≠0,④
△2>0,即有12•
-4>0,⑤
从而k1∈(-
,-
)∪(
,
)且k1≠±1;
②A1为双曲线的一个顶点,则k1=
,
由弦长公式得|A2B2|=
•
=
•
=2
.
| 2 |
联立得y=k1(x+
| 2 |
消去y得(k12-1)x2+2
| 2 |
根据题意得k12-1≠0,②
△1>0,即有12k12-4>0.③
完全类似地有
| 1 |
| k12 |
△2>0,即有12•
| 1 |
| k12 |
从而k1∈(-
| 3 |
| ||
| 3 |
| ||
| 3 |
| 3 |
②A1为双曲线的一个顶点,则k1=
| ||
| 2 |
由弦长公式得|A2B2|=
1+
|
|
| 1+2 |
|
| 30 |
点评:本题主要考查了直线与圆锥曲线的交点,考查弦长公式,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
“B=60°”是“△ABC三个内角成等差数列”的( )
| A、充分非必要条件 |
| B、充要条件 |
| C、必要非充分条件 |
| D、既不充分又非必要条件. |
如图,已知AB⊥平面BCD,BC⊥CD,则图中直角三角形的个数为( )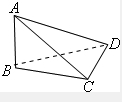

| A、1 | B、2 | C、3 | D、4 |