题目内容
设等差数列{an}的前n项和为Sn，若S3=9，S9=36，则a7+a8+a9等于（ ）
| A、15 | B、12 | C、36 | D、27 |
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：由等差数列性质知S3、S6-S3、S9-S6成等差数列，求出S6，即可求出a7+a8+a9此题考查学生灵活运用等差数列的性质化简求值，是一道中档题．．
解答：
解：由等差数列性质知S3、S6-S3、S9-S6成等差数列，即9，S6-9，36-S6成等差，
∴2（S6-9）=9+36-S6，
∴S6=21
∴S9-S6=15，
∴a7+a8+a9=15
故选：A．
∴2（S6-9）=9+36-S6，
∴S6=21
∴S9-S6=15，
∴a7+a8+a9=15
故选：A．
点评：此题考查学生灵活运用等差数列的性质化简求值，是一道中档题．
练习册系列答案
相关题目
已知α是第一象限角，那么
是（ ）
| α |
| 2 |
| A、第一象限角 |
| B、第二象限角 |
| C、第一或第二象限角 |
| D、第一或第三象限角 |
函数y=㏑（x-1）在区间（1，+∞）内是（ ）
| A、单调递增 | B、单调递减 |
| C、有极小值 | D、有极大值 |
设x，y满足的约束条件是
，则z=x+2y的最小值是（ ）
|
| A、-1 | B、3 | C、5 | D、6 |
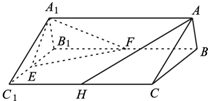如图，在直三棱柱ABC-A1B1C1中，AB=AC=1，AA1=2，E、F分别是棱B1C1、B1B的中点，H在棱CC1上，且AB⊥AH．