题目内容
函数y=㏑（x-1）在区间（1，+∞）内是（ ）
| A、单调递增 | B、单调递减 |
| C、有极小值 | D、有极大值 |
考点：复合函数的单调性
专题：函数的性质及应用
分析：由于函数t=x-1在区间（1，+∞）内是增函数，且t＞0，再结合复合函数的单调性可得结论．
解答：
解：由于函数t=x-1在区间（1，+∞）内是增函数，且t＞0，
故函数y=㏑（x-1）在区间（1，+∞）内是增函数，
故选：A．
故函数y=㏑（x-1）在区间（1，+∞）内是增函数，
故选：A．
点评：本题主要考查复合函数的单调性，对数函数的定义域，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
下列各组函数中，表示相等函数的是（ ）
A、y=
| |||||
| B、y=lnex与y=elnx | |||||
C、y=
| |||||
D、y=x0与y=
|
曲线y=x3+x-2在点P0处的切线平行于直线y=4x-1，则点P0的坐标是（ ）
| A、（0，1） |
| B、（-1，-5） |
| C、（1，0）或（-1，-4） |
| D、（0，1）或（4，1） |
用三种不同的颜色填涂如图中的6个区域，要求每行、每列的区域都不同色，则不同的填涂方法种数共有（ ）| A、12 | B、24 | C、12 | D、6 |
图中阴影部分区域所表示的不等式组是（ ）
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
“a＞b”是“ac2＞bc2”的（ ）
| A、充分条件 |
| B、必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设等差数列{an}的前n项和为Sn，若S3=9，S9=36，则a7+a8+a9等于（ ）
| A、15 | B、12 | C、36 | D、27 |
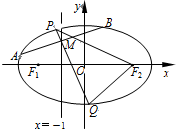如图，F1、F2是离心率为