题目内容
已知函数f(x)=
x3-x,数列{an}满足条件:a1≥1,an+1≥f′(an+1).试用数学归纳法证明:an≥2n-1.
| 1 |
| 3 |
考点:数学归纳法
专题:点列、递归数列与数学归纳法
分析:依题意,a1≥1,an+1≥(an+1)2-1,利用数学归纳法证明:(1)当n=1时,易证结论成立;(2)假设n=k(k≥1)且k∈N*时结论成立,即ak≥2k-1,去证明当n=k+1时,结论也成立即可.
解答:
解:∵f(x)=x2-1,an+1≥f′(an+1),
∴an+1≥(an+1)2-1…(3分)
下面用数学归纳法证明:
(1)当n=1时,a1≥21-1=1,结论成立;…(5分)
(2)假设n=k(k≥1)且k∈N*时结论成立,即ak≥2k-1,…(6分)
则当n=k+1时,ak+1≥(ak+1)2-1≥22k-1≥2k+1-1…(9分)
即n=k+1时,结论也成立.…(11分)
由(1)、(2)知,对任意n∈N*,都有an≥2n-1.…(12分)
∴an+1≥(an+1)2-1…(3分)
下面用数学归纳法证明:
(1)当n=1时,a1≥21-1=1,结论成立;…(5分)
(2)假设n=k(k≥1)且k∈N*时结论成立,即ak≥2k-1,…(6分)
则当n=k+1时,ak+1≥(ak+1)2-1≥22k-1≥2k+1-1…(9分)
即n=k+1时,结论也成立.…(11分)
由(1)、(2)知,对任意n∈N*,都有an≥2n-1.…(12分)
点评:本题考查数学归纳法,着重考查推理与证明的能力,证明当n=k+1时,合理放缩是关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设等差数列{an}的前n项和为Sn,若S3=9,S9=36,则a7+a8+a9等于( )
| A、15 | B、12 | C、36 | D、27 |
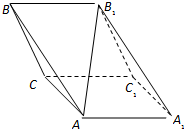 如图,斜三棱柱ABC-A1B1C1,已知侧面BB1C1C与底面ABC垂直且∠BCA=90°,∠B1BC=60°,BC=BB1=2,若二面角A-B1B-C为30°,
如图,斜三棱柱ABC-A1B1C1,已知侧面BB1C1C与底面ABC垂直且∠BCA=90°,∠B1BC=60°,BC=BB1=2,若二面角A-B1B-C为30°,