题目内容
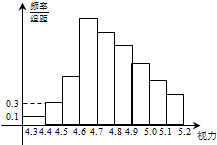 为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6至5.0之间的学生为b,求a,b的值.
为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6至5.0之间的学生为b,求a,b的值.考点:频率分布直方图
专题:等差数列与等比数列,概率与统计
分析:根据频率分布直方图,结合等差、等比数列的知识,求出a、b的值.
解答:
解:根据频率分布直方图,得;
各组组距为4.5-4.4=0.1,
4.3~4.4之间的频数为100×0.1×0.1=1,
4.4~4.5之间的频数为100×0.1×0.3=3,
根据前4组的频数成等比数列,得4.6~4.7之间的频数为1•(
)3=27,
∴最大频率a=
=0.27;
根据后6组频数成等差数列,且有100-13=87(人),设公为d,
则6×27+
d=87,
解得d=-5;
∴b=4×27+
×(-5)=78;
综上,a=0.27,b=78.
各组组距为4.5-4.4=0.1,
4.3~4.4之间的频数为100×0.1×0.1=1,
4.4~4.5之间的频数为100×0.1×0.3=3,
根据前4组的频数成等比数列,得4.6~4.7之间的频数为1•(
| 3 |
| 1 |
∴最大频率a=
| 27 |
| 100 |
根据后6组频数成等差数列,且有100-13=87(人),设公为d,
则6×27+
| 6×5 |
| 2 |
解得d=-5;
∴b=4×27+
| 4×3 |
| 2 |
综上,a=0.27,b=78.
点评:本题考查了频率分布直方图的应用问题,也考查了等差与等比数列的应用问题,是综合题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
在数列{an}中,a1=2且对任意正整数n,an+1-2an=0,数列{an}的前n项和为Sn,bn是Sn与Sn+1的等差中项,则b5=( )
| A、96 | B、94 |
| C、188 | D、192 |
已知两个非零向量
=(m-1,n-1)和
(m-3,n-3),若cos<
,
>≤0,则m+n的取值范围是( )
| a |
| b |
| a |
| b |
A、[
| ||||
| B、[2,6] | ||||
C、(
| ||||
| D、(2,6) |
设f(x)在x=x°处可导,且
=1,则f′(x0)等于( )
| lim |
| △x→0 |
| f(x0+3△x)-f(x0) |
| △x |
| A、1 | ||
| B、0 | ||
| C、3 | ||
D、
|
已知f(x)是偶函数,在(0,+∞)上为减函数,若f(
)>0>f(
),则f(x)=0的根的个数为( )
| 1 |
| 2 |
| 3 |
| A、2个 |
| B、2个或 1个 |
| C、3个 |
| D、2个或3个 |