题目内容
设f(x)在x=x°处可导,且
=1,则f′(x0)等于( )
| lim |
| △x→0 |
| f(x0+3△x)-f(x0) |
| △x |
| A、1 | ||
| B、0 | ||
| C、3 | ||
D、
|
考点:导数的运算
专题:导数的概念及应用
分析:根据得到的定义,
=3
=3f′(x0),问题得以解决
| lim |
| △x→0 |
| f(x0+3△x)-f(x0) |
| △x |
| lim |
| △x→0 |
| f(x0+3△x)-f(x0) |
| 3△x |
解答:
解:
=3
=3f′(x0)=1,
∴f′(x0)=
,
故选:D
| lim |
| △x→0 |
| f(x0+3△x)-f(x0) |
| △x |
| lim |
| △x→0 |
| f(x0+3△x)-f(x0) |
| 3△x |
∴f′(x0)=
| 1 |
| 3 |
故选:D
点评:本题考查了导数的定义,属于基础题

练习册系列答案
相关题目
函数极限
的值为( )
| lim |
| x→x0 |
ln
| ||||
| x-x0 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,三内角A、B、C所对的边分别为a、b、c,已知内角C为钝角,向量
=(2sinA,-1),
=(sinA,cos2A+2)且
⊥
.
(1)试求角A的大小;
(2)试比较b+c与
a的大小.
| m |
| n |
| m |
| n |
(1)试求角A的大小;
(2)试比较b+c与
| 3 |
函数f(x)=lnx-x+2的零点个数为( )
| A、0个 | B、1个 | C、2个 | D、3个 |
在△ABC中,“cosA=2sinBsinC”是“△ABC为钝角三角形”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
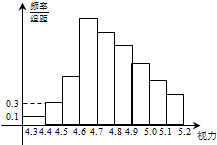 为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6至5.0之间的学生为b,求a,b的值.
为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6至5.0之间的学生为b,求a,b的值.