题目内容
已知f(x)是偶函数,在(0,+∞)上为减函数,若f(
)>0>f(
),则f(x)=0的根的个数为( )
| 1 |
| 2 |
| 3 |
| A、2个 |
| B、2个或 1个 |
| C、3个 |
| D、2个或3个 |
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:根据函数奇偶性和单调性之间的关系,即可得到结论.
解答:
解:∵f(x)在(0,+∞)上为减函数,若f(
)>0>f(
),
∴在(
,
)内方程f(x)=0存在唯一的一个根,
∵f(x)是偶函数,∴根据对称性,则(-
,-
)内方程f(x)=0存在唯一的一个根,
故f(x)=0的根的个数为2个,
故选:A
| 1 |
| 2 |
| 3 |
∴在(
| 1 |
| 2 |
| 3 |
∵f(x)是偶函数,∴根据对称性,则(-
| 3 |
| 1 |
| 2 |
故f(x)=0的根的个数为2个,
故选:A
点评:本题主要考查方程根的个数的判断,根据函数单调性和奇偶性的关系是解决本题的关键.

练习册系列答案
相关题目
函数f(x)=lnx-x+2的零点个数为( )
| A、0个 | B、1个 | C、2个 | D、3个 |
给出以下四个命题:
(1)若x2-5x+6=0,则x=2或x=3;
(2)若2≤x<3,则(x-2)(x-3)≤0;
(3)若a=b=0,则|a|+|b|=0;
(4)若x,y∈N,x+y是奇数,则x,y中一个是奇数,一个是偶数.
那么 ( )
(1)若x2-5x+6=0,则x=2或x=3;
(2)若2≤x<3,则(x-2)(x-3)≤0;
(3)若a=b=0,则|a|+|b|=0;
(4)若x,y∈N,x+y是奇数,则x,y中一个是奇数,一个是偶数.
那么 ( )
| A、(4)的逆命题假 |
| B、(1)的逆命题真 |
| C、(2)的否命题真 |
| D、(3)的否命题假 |
在△ABC中,“cosA=2sinBsinC”是“△ABC为钝角三角形”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知
+
=1(m>0,n>0),则当m+n取得最小值时,椭圆
+
=1的方程为( )
| 1 |
| m |
| 2 |
| n |
| x2 |
| m |
| y2 |
| n |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
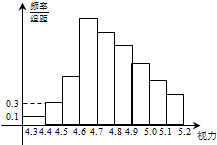 为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6至5.0之间的学生为b,求a,b的值.
为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6至5.0之间的学生为b,求a,b的值.