题目内容
掷红、白两颗骰子，事件A={红骰子点数小于3}，事件B={白骰子点数小于3}，则事件P（A∩B）= ，P（A∪B）= ．
考点：互斥事件的概率加法公式
专题：概率与统计
分析：利用列举法，列举事件A，事件B，根据概率公式计算即可
解答：
解：由掷红、白两颗骰子，向上的点数共6×6=36种可能，红色骰子的点数分别记为红1，红2，…，白色骰子的点数分别记为白1，白2，…
其中红骰子点数小于3的有1，2二种可能，其中白骰子点数小于3的有1，2二种可能，
事件A={红1，白1}，{红1，白2}，{红1，白3}，{红1，白4}，{红1，白5}，{红1，白6}，
{红2，白1}，{红2，白2}，{红2，白3}，{红2，白4}，{红2，白5}，{红2，白6}，共12种
事件B={白1，红1}，{白1，红2}，{白1，红3}，{白1，红4}，{白1，红5}，{白1，红6}
{白2，红1}，{白2，红2}，{白2，红3}，{白2，红4}，{白2，红5}，{白2，红6}，共12种，
事件（A∩B）={红1，白1}，{红1，白2}，{红2，白1}，{红2，白2}，共4种，
故P（A∩B）=
=
故P（B）=
=
，
时间（A∪B）共有12+12-4=20种，
故P（A∪B）=
=
故答案为：
，
其中红骰子点数小于3的有1，2二种可能，其中白骰子点数小于3的有1，2二种可能，
事件A={红1，白1}，{红1，白2}，{红1，白3}，{红1，白4}，{红1，白5}，{红1，白6}，
{红2，白1}，{红2，白2}，{红2，白3}，{红2，白4}，{红2，白5}，{红2，白6}，共12种
事件B={白1，红1}，{白1，红2}，{白1，红3}，{白1，红4}，{白1，红5}，{白1，红6}
{白2，红1}，{白2，红2}，{白2，红3}，{白2，红4}，{白2，红5}，{白2，红6}，共12种，
事件（A∩B）={红1，白1}，{红1，白2}，{红2，白1}，{红2，白2}，共4种，
故P（A∩B）=
| 4 |
| 36 |
| 1 |
| 9 |
故P（B）=
| 2 |
| 6 |
| 1 |
| 3 |
时间（A∪B）共有12+12-4=20种，
故P（A∪B）=
| 20 |
| 36 |
| 5 |
| 9 |
故答案为：
| 1 |
| 9 |
| 5 |
| 9 |
点评：本题考查古典概型的求解，涉及概率的基本性质和概率公式，属基础题．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
某商品的价格前两年每年递增20%，后两年每年递减20%，最后一年的价格与原来的价格比较，变化情况是（ ）
| A、不增不减 |
| B、约增1.4% |
| C、约减9.2% |
| D、约减7.8% |
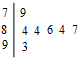如图是 a，b年在某大学自主招生面试环节中，七位评委为某考生打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的平均数和方差分别为（ ）| A、83，1.5 |
| B、84，1.5 |
| C、85，1.6 |
| D、86，1.6 |
函数极限
的值为（ ）
| lim |
| x→x0 |
ln
| ||||
| x-x0 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
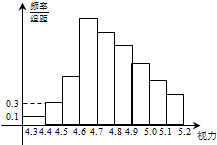为了解某校高三学生的视力情况，随机地抽查了该校100名高三学生的视力情况，得到频率分布直方图，由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频数成等差数列，设最大频率为a，视力在4.6至5.0之间的学生为b，求a，b的值．函数f（x）=lnx-x+2的零点个数为（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |