题目内容
在数列{an}中,a1=2且对任意正整数n,an+1-2an=0,数列{an}的前n项和为Sn,bn是Sn与Sn+1的等差中项,则b5=( )
| A、96 | B、94 |
| C、188 | D、192 |
考点:数列递推式
专题:等差数列与等比数列
分析:由an+1-2an=0得到an+1=2an,即数列{an}是等比数列,根据等比数列的性质和公式即可得到结论.
解答:
解:由an+1-2an=0得到an+1=2an,即数列{an}是公比q=2的等比数列,
则Sn=
=
=2n+1-2,
∵bn是Sn与Sn+1的等差中项,
∴bn=
(Sn+Sn+1)=
=2n+2n+1-2,
则b5=25+26-2=94,
故选:B
则Sn=
| a1(1-qn) |
| 1-q |
| 2(1-2n) |
| 1-2 |
∵bn是Sn与Sn+1的等差中项,
∴bn=
| 1 |
| 2 |
| 2n+1-2+2n+2-2 |
| 2 |
则b5=25+26-2=94,
故选:B
点评:本题主要考查递推数列的应用,根据条件得到数列是等比数列是解决本题的关键.

练习册系列答案
相关题目
函数极限
的值为( )
| lim |
| x→x0 |
ln
| ||||
| x-x0 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如果l1、l2两直线的斜率是方程x2-4x+1=0的两实根,那么l1,l2的夹角是( )
| A、60° | B、45° |
| C、30° | D、90° |

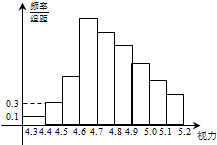 为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6至5.0之间的学生为b,求a,b的值.
为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6至5.0之间的学生为b,求a,b的值.