题目内容
已知两个非零向量
=(m-1,n-1)和
(m-3,n-3),若cos<
,
>≤0,则m+n的取值范围是( )
| a |
| b |
| a |
| b |
A、[
| ||||
| B、[2,6] | ||||
C、(
| ||||
| D、(2,6) |
考点:平面向量数量积的运算,数量积表示两个向量的夹角
专题:计算题,不等式的解法及应用,平面向量及应用
分析:运用向量的夹角公式,可得,(m-1)(m-3)+(n-1)(n-3)≤0,化简配方,再令m-2=rcosα,n-2=rsinα,求得r的范围,再代入m+n,化简整理,运用两角和的正弦公式,结合正弦函数的值域,即可得到.
解答:
解:由于
•
=(m-1)(m-3)+(n-1)(n-3),
且m≠1,n≠1,m≠3,n≠3,
又cos<
,
>≤0,则(m-1)(m-3)+(n-1)(n-3)≤0,
即有(m-2)2+(n-2)2≤2,
可令m-2=rcosα,n-2=rsinα,代入上式,可得,-
≤r≤
,
则m+n=4+r(cosα+sinα)=4+
rsin(α+
),
由于sinα和cosα不能相等或相反,∴-1<sin(α+
)<1,
则有4-2<m+n<4+2,即有2<m+n<6.
故选D.
| a |
| b |
且m≠1,n≠1,m≠3,n≠3,
又cos<
| a |
| b |
即有(m-2)2+(n-2)2≤2,
可令m-2=rcosα,n-2=rsinα,代入上式,可得,-
| 2 |
| 2 |
则m+n=4+r(cosα+sinα)=4+
| 2 |
| π |
| 4 |
由于sinα和cosα不能相等或相反,∴-1<sin(α+
| π |
| 4 |
则有4-2<m+n<4+2,即有2<m+n<6.
故选D.
点评:本题考查用两个向量的数量积表示两个向量的夹角,正弦函数的值域,得到(m-2)2+(n-2)2≤2,是解题的关键.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
函数y=xlnx的单调递减区间是( )
| A、(0,e-1) |
| B、(-∞,e-1) |
| C、(e-1,+∞) |
| D、(e,+∞) |
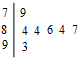 如图是 a,b年在某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
如图是 a,b年在某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A、83,1.5 |
| B、84,1.5 |
| C、85,1.6 |
| D、86,1.6 |
在面积为S的△ABC的边上AC任取一点P1,“使P1BC的面积大于
”的概率等于( )
| S |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设定义域为R的函数f(x),g(x)都有反函数,并且f(x-1)和g-1(2x-2)函数的图象关于直线y=x对称,若g(2)=2008,则f(1)的值为( )
| A、1005 | B、2008 |
| C、1003 | D、以上结果均不对 |
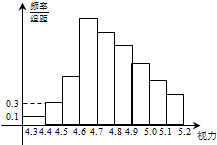 为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6至5.0之间的学生为b,求a,b的值.
为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6至5.0之间的学生为b,求a,b的值.