题目内容
8．以双曲线$\frac{{x}^{2}}{3}$-y2=1的左右焦点为焦点，离心率为$\frac{1}{2}$的椭圆的标准方程为（ ）| A． | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{16}$=1 | B． | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{8}$=1 | C． | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1 | D． | $\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{12}$=1 |
分析 求出双曲线的焦点，设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），由题意可得c=2，即有a2-b2=4，又e=$\frac{c}{a}$=$\frac{1}{2}$，解得a，b，即可得到所求椭圆方程．
解答 解：双曲线$\frac{{x}^{2}}{3}$-y2=1的焦点为（±2，0），
设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），
由题意可得c=2，即有a2-b2=4，
又e=$\frac{c}{a}$=$\frac{1}{2}$，
解得a=4，b=2$\sqrt{3}$，
可得椭圆的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1．
故选：C．
点评 本题考查椭圆的方程的求法，注意运用待定系数法，考查双曲线的方程和性质，属于基础题．
练习册系列答案
相关题目
18．数列{an}满足a1=1，且an+1=a1+an+n（n∈N*），则$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2016}}$等于（ ）
| A． | $\frac{2015}{2016}$ | B． | $\frac{4028}{2015}$ | C． | $\frac{4032}{2017}$ | D． | $\frac{2014}{2015}$ |
19．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1，F2，c是半焦轴距，P是双曲线上异于顶点的点，满足ctan∠PF1F2=atan∠PF2F1，则双曲线的离心率e的取值范围是（ ）
| A． | （1，1+$\sqrt{2}$） | B． | （$\sqrt{2}$，1+$\sqrt{2}$） | C． | （1+$\sqrt{2}$，1+$\sqrt{3}$） | D． | （1+$\sqrt{2}$，+∞） |
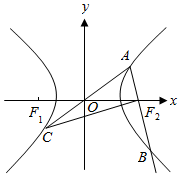如图，点F1、F2为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）的左右焦点，点A、B、C分别为双曲线上三个不同的点，且AC经过坐标原点O，并满足$\overrightarrow{A{F_2}}=\frac{1}{2}\overrightarrow{{F_2}B}$，$\overrightarrow{AB}•\overrightarrow{C{F_2}}=0$，则双曲线的离心率为$\frac{\sqrt{17}}{3}$．
17．已知点F1是抛物线C：x2=4y的焦点，点F2为抛物线C的对称轴与其准线的交点，过F2作抛物线C的切线，切点为A，若点A恰好在以F1，F2为焦点的双曲线上，则双曲线的离心率为（ ）
| A． | $\frac{\sqrt{6}-\sqrt{2}}{2}$ | B． | $\sqrt{2}$-1 | C． | $\sqrt{2}$+1 | D． | $\frac{\sqrt{6}+\sqrt{2}}{2}$ |