题目内容
7.函数f(x)在[a,b]上有定义,若对任意x1,x2∈[a,b],有$f({\frac{{{x_1}+{x_2}}}{2}})≤\frac{1}{2}[{f({x_1})+f({x_2})}]$,则称f(x)在[a,b]上具有性质P.设f(x)在[1,3]上具有性质P,现给出如下命题:①若f(x)在x=2处取得最大值1,则f(x)=1,x∈[1,3];
②对任意x1,x2,x3,x4∈[1,3],有f($\frac{{x}_{1}+{x}_{2}+{x}_{3}+{x}_{4}}{4}$)≤$\frac{1}{4}$[f(x1)+f(x2)+f(x3)+f(x4)].
③f(x)在[1,3]上的图象是连续不断的;
④f(x2)在$[{1,\sqrt{3}}]$上具有性质P;
其中真命题的序号是( )
| A. | ①② | B. | ①③ | C. | ②④ | D. | ③④ |
分析 根据题设条件,分别举出反例,说明①和②都是错误的;同时证明③和④是正确的.
解答 解:在①中:在[1,3]上,f(2)=f( $\frac{x+4-x}{2}$)≤$\frac{1}{2}$[f(x)+f(4-x)],
∴$\left\{\begin{array}{l}{f(x)+f(4-x)≥2}\\{f(x)≤f(x)_{max}=f(2)=1}\\{f(4-x)≤f(x)_{max}=f(2)=1}\end{array}\right.$,
故f(x)=1,
∴对任意的x1,x2∈[1,3],f(x)=1,
故①成立;
在②中,对任意x1,x2,x3,x4∈[1,3],
有f($\frac{{x}_{1}+{x}_{2}+{x}_{3}+{x}_{4}}{4}$)=f( $\frac{\frac{1}{2}({x}_{1}+{x}_{2})+\frac{1}{2}({x}_{3}+{x}_{4})}{2}$)
≤$\frac{1}{2}$[f( $\frac{{x}_{1}+{x}_{2}}{2}$)+f( $\frac{{x}_{3}+{x}_{4}}{2}$ )]
≤$\frac{1}{2}$[$\frac{1}{2}$(f(x1 )+f(x2))+$\frac{1}{2}$(f(x3)+f(x4))]
=$\frac{1}{4}$[f(x1)+f(x2)+f(x3)+f(x4)],
∴f($\frac{{x}_{1}+{x}_{2}+{x}_{3}+{x}_{4}}{4}$)≤$\frac{1}{4}$[f(x1)+f(x2)+f(x3)+f(x4)].
故②成立.
在③中,反例:f(x)=$\left\{\begin{array}{l}{({\frac{1}{3})}^{x},1≤x<3}\\{2,x=3}\end{array}\right.$在[1,3]上满足性质P,
但f(x)在[1,3]上不是连续函数,故③不成立;
在④中,反例:f(x)=-x在[1,3]上满足性质P,但f(x2)=-x2在[1,$\sqrt{3}$]上不满足性质P,
故④不成立;
故选:A.
点评 本题考查的知识点为函数定义的理解,说明一个结论错误时,只需举出反例即可.说明一个结论正确时,要证明对所有的情况都成立.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{\sqrt{6}-\sqrt{2}}{2}$ | B. | $\sqrt{2}$-1 | C. | $\sqrt{2}$+1 | D. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ |
| A. | 128 | B. | ±128 | C. | 64 | D. | ±64 |
| A. | (-2,0) | B. | (-2,-1) | C. | (-$\frac{5}{4}$,0) | D. | (-$\frac{5}{4}$,-1) |
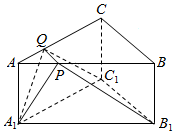 已知在直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,侧棱AA1的长为$\frac{{\sqrt{3}}}{2}$,P、Q分别是AB、AC上的点,且PQ∥BC,如图.
已知在直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,侧棱AA1的长为$\frac{{\sqrt{3}}}{2}$,P、Q分别是AB、AC上的点,且PQ∥BC,如图.