题目内容
12.已知实数x,y满足条件$\left\{\begin{array}{l}y≤x\\ x+y≥2\\ 2x+y≥6\end{array}\right.$,则z=3x+2y的取值范围是( )| A. | (-∞,10] | B. | [5,10] | C. | [8,+∞) | D. | [8,10] |
分析 作出不等式组对应的平面区域,利用目标函数的几何意义,进行求最值即可.
解答 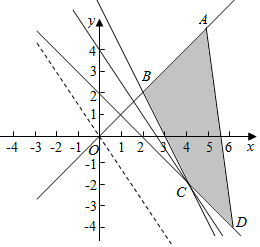 解:由z=3x+2y得$y=-\frac{3}{2}x+\frac{z}{2}$
解:由z=3x+2y得$y=-\frac{3}{2}x+\frac{z}{2}$
作出不等式组对应的平面区域如图(阴影部分):
平移直线$y=-\frac{3}{2}x+\frac{z}{2}$由图象可知当直线$y=-\frac{3}{2}x+\frac{z}{2}$经过点C时,直线$y=-\frac{3}{2}x+\frac{z}{2}$的截距最小,
此时z也最小,无最大值.
由$\left\{\begin{array}{l}{x+y=2}\\{2x+y=6}\end{array}\right.$,解$\left\{\begin{array}{l}{x=4}\\{y=-2}\end{array}\right.$,即C(4,-2)
代入目标函数z=3x+2y,
得z=3×4+2×(-2)=12-4=8.
故z=3x+2y的取值范围是[8,+∞)
故选:
点评 本题主要考查线性规划的基本应用,利用目标函数的几何意义是解决问题的关键,利用数形结合是解决问题的基本方法.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
17.已知点F1是抛物线C:x2=4y的焦点,点F2为抛物线C的对称轴与其准线的交点,过F2作抛物线C的切线,切点为A,若点A恰好在以F1,F2为焦点的双曲线上,则双曲线的离心率为( )
| A. | $\frac{\sqrt{6}-\sqrt{2}}{2}$ | B. | $\sqrt{2}$-1 | C. | $\sqrt{2}$+1 | D. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ |
1.如果执行如图所示的程序框图,那么输出的a=( )


| A. | 2 | B. | $\frac{1}{2}$ | C. | -1 | D. | 以上都不正确 |
2.已知函数f(x)=$\left\{\begin{array}{l}{-x,x≤0}\\{-{x}^{2}+2x,x>0}\end{array}\right.$,若方程f2(x)+bf(x)+$\frac{1}{4}$=0有六个相异实根,则实数b的取值范围( )
| A. | (-2,0) | B. | (-2,-1) | C. | (-$\frac{5}{4}$,0) | D. | (-$\frac{5}{4}$,-1) |
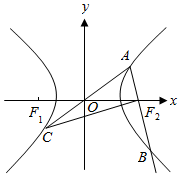 如图,点F1、F2为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的左右焦点,点A、B、C分别为双曲线上三个不同的点,且AC经过坐标原点O,并满足$\overrightarrow{A{F_2}}=\frac{1}{2}\overrightarrow{{F_2}B}$,$\overrightarrow{AB}•\overrightarrow{C{F_2}}=0$,则双曲线的离心率为$\frac{\sqrt{17}}{3}$.
如图,点F1、F2为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的左右焦点,点A、B、C分别为双曲线上三个不同的点,且AC经过坐标原点O,并满足$\overrightarrow{A{F_2}}=\frac{1}{2}\overrightarrow{{F_2}B}$,$\overrightarrow{AB}•\overrightarrow{C{F_2}}=0$,则双曲线的离心率为$\frac{\sqrt{17}}{3}$.