题目内容
2.已知抛物线C:y2=4x,直线l交于A,B两点,O为坐标原点,直线OA,OB的斜率分别为k1,k2,若k1•k2=-2,则△AOB面积的最小值为4$\sqrt{2}$.分析 由题意可设直线AB的方程为:x=my+b,与抛物线方程联立可得根与系数的关系、利用斜率公式得出直线AB过定点M(2,0),再利用三角形的面积计算公式即可得出结论.
解答 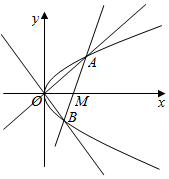 解:由题意可设直线AB的方程为:x=my+b.
解:由题意可设直线AB的方程为:x=my+b.
联立$\left\{\begin{array}{l}{x=my+b}\\{{y}^{2}=4x}\end{array}\right.$,化为y2-4my-4b=0,
∴y1+y2=4m,y1y2=-4b.
∵直线OA,OB的斜率分别为k1,k2,k1•k2=-2.
∴$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=-2.
∴y1y2=-8,
∴-4b=-8,
∴b=2.
因此直线AB过定点M(2,0).
∴△AOB面积S=$\frac{1}{2}×2×$|y1-y2|=$\sqrt{16{m}^{2}+32}$
因此当m=0时,△AOB的面积取得最小值4$\sqrt{2}$.
故答案为:4$\sqrt{2}$.
点评 本题综合考查了直线与抛物线相交问题转化为方程联立可得根与系数的关系、斜率公式、三角形的面积计算公式等基础知识与基本技能方法,考查了推理能力和计算能力,属于中档题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
10.阅读如图的程序框图,当该程序运行后输出的x值是( )
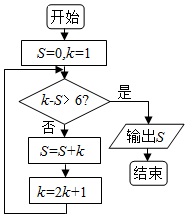

| A. | 57 | B. | 63 | C. | 110 | D. | 120 |
17.已知点F1是抛物线C:x2=4y的焦点,点F2为抛物线C的对称轴与其准线的交点,过F2作抛物线C的切线,切点为A,若点A恰好在以F1,F2为焦点的双曲线上,则双曲线的离心率为( )
| A. | $\frac{\sqrt{6}-\sqrt{2}}{2}$ | B. | $\sqrt{2}$-1 | C. | $\sqrt{2}$+1 | D. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ |
7.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)两条渐近线的夹角为60°,则该双曲线的离心率为( )
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{{2\sqrt{3}}}{3}$或2 | D. | 4 |
14.设α,β,γ为平面,m,n,l为直线,则m⊥β的一个充分条件是( )
| A. | α⊥β,α∩β=l,m⊥l | B. | n⊥α,m⊥α,n⊥β | C. | α⊥γ,β⊥γ,m⊥α | D. | α⊥γ,α∩γ=m,β⊥γ |