题目内容
5.某地区18岁的女青年的血压服从正态分布N(110,122).在该地区随机地选一女青年,测量她的血压X,求P{X≤105},P{100<X≤120};确定最小的x,使P{X>x}≤0.05.(结果用Φ(x)或其反函数表示)分析 (1)利用P{X≤105}=P{$\frac{X-110}{12}$≤-$\frac{5}{12}$},P{100<X≤120}=Φ($\frac{120-110}{12}$)-Φ($\frac{100-110}{12}$),即可得出结论;
(2)使P{X>x}≤0.05,求x,即1-P{X≤x}≤0.05,亦即Φ($\frac{x-110}{12}$)≥0.95,可得结论.
解答 解:已知血压X~N(110,122).
(1)P{X≤105}=P{$\frac{X-110}{12}$≤-$\frac{5}{12}$}≈1-Φ(0.42)=0.3372,
P{100<X≤120}=Φ($\frac{120-110}{12}$)-Φ($\frac{100-110}{12}$)
=Φ(0.833)-Φ(-0.833)=2Φ(0.833)-1≈0.595.
(2)使P{X>x}≤0.05,求x,即1-P{X≤x}≤0.05,亦即Φ($\frac{x-110}{12}$)≥0.95,
查表得$\frac{x-110}{12}$≥1.645,从而x≥129.74.
点评 本题考查概率的计算,考查学生转化问题的能力,正确转化是关键.

练习册系列答案
相关题目
10.阅读如图的程序框图,当该程序运行后输出的x值是( )
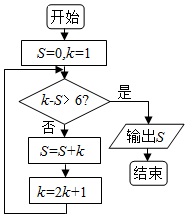

| A. | 57 | B. | 63 | C. | 110 | D. | 120 |
17.已知点F1是抛物线C:x2=4y的焦点,点F2为抛物线C的对称轴与其准线的交点,过F2作抛物线C的切线,切点为A,若点A恰好在以F1,F2为焦点的双曲线上,则双曲线的离心率为( )
| A. | $\frac{\sqrt{6}-\sqrt{2}}{2}$ | B. | $\sqrt{2}$-1 | C. | $\sqrt{2}$+1 | D. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ |
14.设α,β,γ为平面,m,n,l为直线,则m⊥β的一个充分条件是( )
| A. | α⊥β,α∩β=l,m⊥l | B. | n⊥α,m⊥α,n⊥β | C. | α⊥γ,β⊥γ,m⊥α | D. | α⊥γ,α∩γ=m,β⊥γ |
15.在1和16之间插入3个数,使它们与这两个数依次构成等比数列,则这3个数的积( )
| A. | 128 | B. | ±128 | C. | 64 | D. | ±64 |
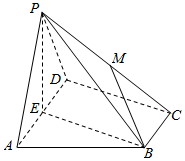 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,M是棱PC的中点,PA=PD=2,$BC=\frac{1}{2}AD=1$,$CD=\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,M是棱PC的中点,PA=PD=2,$BC=\frac{1}{2}AD=1$,$CD=\sqrt{3}$.