题目内容
证明下列命题:
(1)若函数f(x)可导且为周期函数,则f′(x)也为周期函数;
(2)可导的奇函数的导函数是偶函数.
(1)若函数f(x)可导且为周期函数,则f′(x)也为周期函数;
(2)可导的奇函数的导函数是偶函数.
考点:简单复合函数的导数,导数的运算
专题:函数的性质及应用,导数的概念及应用
分析:(1)利用复合函数导数公式及周期性定义即可证明;
(2)利用复合函数导数公式及奇偶性定义即可证明;
(2)利用复合函数导数公式及奇偶性定义即可证明;
解答:
证明:(1)设f(x)的周期为T,则f(x)=f(x+T).
∴f′(x)=[f(x+T)]′=f′(x+T)•(x+T)′
=f′(x+T),即f′(x)为周期函数且周期与f(x)的周期相同.…(5分)
(2)∵f(x)为奇函数,
∴f(-x)=-f(x).
∴[f(-x)]′=[-f(x)]′.
∴f′(-x)•(-x)′=-f′(x).
∴f′(-x)=f′(x),即f′(x)为偶函数 …(10分)
∴f′(x)=[f(x+T)]′=f′(x+T)•(x+T)′
=f′(x+T),即f′(x)为周期函数且周期与f(x)的周期相同.…(5分)
(2)∵f(x)为奇函数,
∴f(-x)=-f(x).
∴[f(-x)]′=[-f(x)]′.
∴f′(-x)•(-x)′=-f′(x).
∴f′(-x)=f′(x),即f′(x)为偶函数 …(10分)
点评:本题考查复合函数的求导公式及周期性及奇偶性的证明,有一定的综合性

练习册系列答案
相关题目
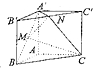 如图,直三角棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=
如图,直三角棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=