题目内容
若不等式x2+kx+4＜0在x∈（1，2）时恒成立，求k的取值范围．
考点：函数恒成立问题
专题：函数的性质及应用
分析：把给出的不等式移向，然后两边同时乘以
，然后由函数x+
的单调性求出-（x+
）的取值范围，则答案可求．
| 1 |
| x |
| 4 |
| x |
| 4 |
| x |
解答：
解：由x2+kx+4＜0在x∈（1，2）时恒成立，得：
kx＜-x2-4在x∈（1，2）时恒成立，
即k＜-x-
在x∈（1，2）时恒成立，
令t=-x-
=-（x+
），
当x∈（1，2）时，x+
为减函数，
∴t∈（-5，-4）．
则k≤-5．
∴k的取值范围是（-∞，-5]．
kx＜-x2-4在x∈（1，2）时恒成立，
即k＜-x-
| 4 |
| x |
令t=-x-
| 4 |
| x |
| 4 |
| x |
当x∈（1，2）时，x+
| 4 |
| x |
∴t∈（-5，-4）．
则k≤-5．
∴k的取值范围是（-∞，-5]．
点评：本题考查函数恒成立问题，考查了分离变量法，训练了y=x+
（k＞0）型函数的单调性，是中档题．
| k |
| x |
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
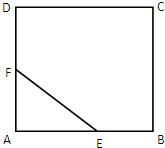如图，有一块正方形区域ABCD，现在要划出一个直角三角形AEF区域进行绿化，满足：EF=1米，设角AEF=θ，θ∈[