题目内容
 某工厂有25周岁以上(含2S周岁)工人300名,25周岁以下工人200名为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100),分别加以统计,得到如图所示的频率分布直方图.
某工厂有25周岁以上(含2S周岁)工人300名,25周岁以下工人200名为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100),分别加以统计,得到如图所示的频率分布直方图.(1)求样本中“25周岁以上(含25周岁)组”抽取的人数、日生产量平均数:
(2)若“25周岁以上组”中日平均生产90件及90件以上的称为“生产能手”;“25周岁以下组”中日平均生产不足60件的称为“菜鸟”.从样本中的“生产能手”和”菜鸟”中任意抽取2人,求这2人日平均生产件数之和X的分布列及期望.(“生产能手”日平均生产件数视为95件,“菜鸟”日平均生产件数视为55件).
考点:离散型随机变量的期望与方差,频率分布直方图
专题:概率与统计
分析:(1)由样本单元数和总体中“25周岁以上(含25周岁)组”的频率,能求出“25周岁以上(含25周岁)组”抽取的人数;利用“255周岁以上组”频率分布直方图能求出“25周岁以上(含25周岁)组”日生产量平均数.
(2)利用频率分布直方图能求出样本中“25周岁以上组”中日平均生产90件及90件以的“生产能手”工人有3人,“25周岁以下组”中日平均生产不足60件的“菜鸟”工人有2人,从这5人组成的样本中,任取2人,这两人的日平均生产件数之和X的可能取值为190,150,110,分别求出P(X=190),P(X=150),P(X=110),由此能求出X的概率分布列和数学期望.
(2)利用频率分布直方图能求出样本中“25周岁以上组”中日平均生产90件及90件以的“生产能手”工人有3人,“25周岁以下组”中日平均生产不足60件的“菜鸟”工人有2人,从这5人组成的样本中,任取2人,这两人的日平均生产件数之和X的可能取值为190,150,110,分别求出P(X=190),P(X=150),P(X=110),由此能求出X的概率分布列和数学期望.
解答:
解:(1)由已知得,样本中有25周岁以上组工人100×
=60名,
样本中“25周岁以上(含25周岁)组”的日生产量平均数为:
55×0.05+65×0.35+75×0.35+85×0.2+95×0.05=73.5.
(2)由题设知,样本中“25周岁以上组”中日平均生产90件及90件以的“生产能手”工人有60×0.05=3人,
“25周岁以下组”中日平均生产不足60件的“菜鸟”工人有40×0.05=2人,
则从日平均生产95件的3名“生产能手”和日平均生产55件的2名“菜鸟”这5人组成的样本中,
任取2人,这两人的日平均生产件数之和X的可能取值为190,150,110,
P(X=190)=
=
,
P(X=150)=
=
,
P(X=110)=
=
,
∴X的概率分布列为:
X的期望EX=190×
+150×
+110×
=158.
| 300 |
| 500 |
样本中“25周岁以上(含25周岁)组”的日生产量平均数为:
55×0.05+65×0.35+75×0.35+85×0.2+95×0.05=73.5.
(2)由题设知,样本中“25周岁以上组”中日平均生产90件及90件以的“生产能手”工人有60×0.05=3人,
“25周岁以下组”中日平均生产不足60件的“菜鸟”工人有40×0.05=2人,
则从日平均生产95件的3名“生产能手”和日平均生产55件的2名“菜鸟”这5人组成的样本中,
任取2人,这两人的日平均生产件数之和X的可能取值为190,150,110,
P(X=190)=
| ||
|
| 3 |
| 10 |
P(X=150)=
| ||||
|
| 3 |
| 5 |
P(X=110)=
| ||
|
| 1 |
| 10 |
∴X的概率分布列为:
| X | 190 | 150 | 110 | ||||||
| P |
|
|
|
| 3 |
| 10 |
| 3 |
| 5 |
| 1 |
| 10 |
点评:本题考查离散型随机变量的概率分布列和数学期望的求法,考查频率分布直方图的应用,解题时要注意排列组合知识的合理运用.

练习册系列答案
相关题目
直线l与圆x2+y2+2x-4y+1=0相交于A,B两点,若弦AB的中点(-2,3),则直线l的方程为( )
| A、x+y-3=0 |
| B、x+y-1=0 |
| C、x-y+5=0 |
| D、x-y-5=0 |
直线l:(2-m)x+(m+1)y-3=0与圆C:(x-2)2+(y-3)2=9的交点个数为( )
| A、2 | B、1 | C、0 | D、与m有关 |
若sinα-2cosα=0,则2sin2α-3sinαcosα-5cos2α+2的值为( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
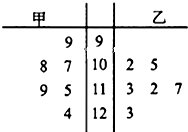 在数学趣味知识培训活动中,甲、乙两名学生的6次培训成绩如茎叶图所示:
在数学趣味知识培训活动中,甲、乙两名学生的6次培训成绩如茎叶图所示: