题目内容
过椭圆
+
=1的左焦点作直线交椭圆于A(x1,y1),B(x2,y2)两点,若x1+x2=-1,则|AB|的值为 .
| x2 |
| 4 |
| y2 |
| 3 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设直线AB:y=k(x+1),联立椭圆方程,消去y得,(3+4k2)x2+8k2x+4k2-12=0,运用韦达定理,由条件x1+x2=-1,求得k,再由弦长公式|AB|=
•
,即可得到答案.
| 1+k2 |
| (x1+x2)2-4x1x2 |
解答:
解:椭圆
+
=1的左焦点为(-1,0),
设直线AB:y=k(x+1),联立椭圆方程,消去y得,
(3+4k2)x2+8k2x+4k2-12=0,
则x1+x2=
,x1x2=
,
由x1+x2=-1,则k2=
,x1x2=
=-
.
则|AB|=
•
=
•
=
.
故答案为:
.
| x2 |
| 4 |
| y2 |
| 3 |
设直线AB:y=k(x+1),联立椭圆方程,消去y得,
(3+4k2)x2+8k2x+4k2-12=0,
则x1+x2=
| -8k2 |
| 3+4k2 |
| 4k2-12 |
| 3+4k2 |
由x1+x2=-1,则k2=
| 3 |
| 4 |
| 3-12 |
| 3+3 |
| 3 |
| 2 |
则|AB|=
| 1+k2 |
| (x1+x2)2-4x1x2 |
=
1+
|
1+4×
|
| 7 |
| 2 |
故答案为:
| 7 |
| 2 |
点评:本题考查椭圆的方程和性质,考查联立直线方程和椭圆方程,消去一个未知数,运用韦达定理和弦长公式解题,考查运算能力,属于中档题.

练习册系列答案
相关题目
已知:A={x|y=2x+1}、B={(x,y)|x+4y=13}.则A∩B=( )
| A、{1,3} | |||||
| B、∅ | |||||
C、{(x,y)|
| |||||
| D、{(1,3)} |
a,b是异面直线,点P∉a∪b,下列命题:
(1)过P可作平面与a,b均平行;
(2)过P可作直线与a,b都相交;
(3)过P可作平面与a,b都垂直;
(4)过P可作直线a,b都垂直,
其中真命题的个数是( )
(1)过P可作平面与a,b均平行;
(2)过P可作直线与a,b都相交;
(3)过P可作平面与a,b都垂直;
(4)过P可作直线a,b都垂直,
其中真命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
一个几何体的三视图如图所示,其侧视图是等边三角形,则该几何体的体积等于( )


A、4
| ||
B、3
| ||
C、2
| ||
D、
|
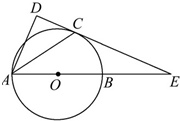 如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.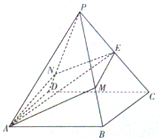 如图,正四棱锥P-ABCD的高为3,底面边长为2,E是棱PC的中点,过AE作平面与棱PB、PD分别交于点M、N(M、N可以是棱的端点).
如图,正四棱锥P-ABCD的高为3,底面边长为2,E是棱PC的中点,过AE作平面与棱PB、PD分别交于点M、N(M、N可以是棱的端点).