题目内容
求点P(2,1)到直线(2k-1)x-(k+3)y-(k-11)=0的最远距离.
考点:点到直线的距离公式
专题:计算题,直线与圆
分析:将直线化为k(2x-y-1)-(x+3y-11)=0,令
解得定点Q,再由PQ垂直于直线时,P到直线的距离最远,由两点的距离公式,即可得到.
|
解答:
解:直线(2k-1)x-(k+3)y-(k-11)=0,
即为k(2x-y-1)-(x+3y-11)=0,
令
解得,
,
即有直线恒过定点Q(2,3).
由直角边小于等于斜边,可得,
当PQ垂直于直线时,P到直线的距离最远,
且为
=2.
即为k(2x-y-1)-(x+3y-11)=0,
令
|
|
即有直线恒过定点Q(2,3).
由直角边小于等于斜边,可得,
当PQ垂直于直线时,P到直线的距离最远,
且为
| (2-2)2+(3-1)2 |
点评:本题考查直线恒过定点的问题,考查点到直线的距离的最大问题,考查运算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知集合A={x|x2-2x<0},B={y|y=2x,x>0},R是实数集,则(∁RB)∩A等于( )
| A、[0,1] |
| B、(0,1] |
| C、(-∞,0] |
| D、[1,+∞] |
直线y=kx分抛物线y=x-x2与x轴所围图形为面积相等的两部分,则直线与抛物线交点的横坐标为( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
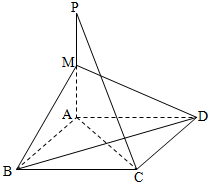 如图,四边形ABCD是菱形,PA⊥平面ABCD,M为PA的中点.
如图,四边形ABCD是菱形,PA⊥平面ABCD,M为PA的中点.