题目内容
直线y=kx分抛物线y=x-x2与x轴所围图形为面积相等的两部分,则直线与抛物线交点的横坐标为( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:如图所示,令x-x2=0,解得x=0,1.联立
,解得O(0,0),B(1-k,k-k2).由于直线y=kx分抛物线y=x-x2与x轴所围图形为面积相等的两部分,
利用微积分基本定理即可得出:
(x-x2)dx=2
(x-x2-kx)dx,解出即可.
|
利用微积分基本定理即可得出:
| ∫ | 1 0 |
| ∫ | 1-k 0 |
解答:
解:如图所示,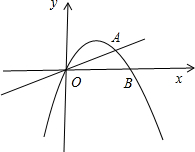
令x-x2=0,解得x=0,1.
联立
,
解得O(0,0),B(1-k,k-k2).
∵直线y=kx分抛物线y=x-x2与x轴所围图形为面积相等的两部分,
∴
(x-x2)dx=2
(x-x2-kx)dx,
∴(
x2-
x3)
=2(
x2-
x3-
kx2)dx,
化为
=2[
-
(1-k)3],
∴1-k=
.
∴直线与抛物线交点的横坐标为
.
故选:C.

令x-x2=0,解得x=0,1.
联立
|
解得O(0,0),B(1-k,k-k2).
∵直线y=kx分抛物线y=x-x2与x轴所围图形为面积相等的两部分,
∴
| ∫ | 1 0 |
| ∫ | 1-k 0 |
∴(
| 1 |
| 2 |
| 1 |
| 3 |
| | | 1 0 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
化为
| 1 |
| 6 |
| (1-k)3 |
| 3 |
| 1 |
| 2 |
∴1-k=
| 3 |
| ||
∴直线与抛物线交点的横坐标为
| 3 |
| ||
故选:C.
点评:本题考查了直线与抛物线相交问题、微积分基本定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
以双曲线的焦点为圆心,实轴长为半径的圆与双曲线的渐近线相切,则双曲线的离心率为( )
A、
| ||
B、
| ||
C、
| ||
| D、2 |
