题目内容
19.已知函数f(x)=sin2x+$\sqrt{3}$sin($\frac{π}{2}$+2x)(1)求函数f(x)的最小正周期;
(2)求函数f(x)的单凋增区间;
(3)求函数f(x)的最大值和最小值及相应的x的值.
分析 (1)由三角函数公式化简可得f(x)=2sin(2x+$\frac{π}{3}$),由周期公式可得;
(2)解2kπ-$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$可得单凋增区间;
(3)当2x+$\frac{π}{3}$分别为2kπ+$\frac{π}{2}$和2kπ-$\frac{π}{2}$,函数取最大、小值,解x可得.
解答 解:(1)由三角函数公式化简可得f(x)=sin2x+$\sqrt{3}$sin($\frac{π}{2}$+2x)
=sin2x+$\sqrt{3}$cos2x=2($\frac{1}{2}$sin2x+$\frac{\sqrt{3}}{2}$cos2x)=2sin(2x+$\frac{π}{3}$)
∴函数f(x)的最小正周期T=$\frac{2π}{2}$=π;
(2)由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$可得kπ-$\frac{5π}{12}$≤x≤kπ+$\frac{π}{12}$,
∴函数f(x)的单凋增区间为[kπ-$\frac{5π}{12}$,kπ+$\frac{π}{12}$](k∈Z);
(3)当2x+$\frac{π}{3}$=2kπ+$\frac{π}{2}$,即x=kπ+$\frac{π}{12}$,k∈Z时,函数f(x)取最大值2;
当2x+$\frac{π}{3}$=2kπ-$\frac{π}{2}$,即x=kπ-$\frac{5π}{12}$,k∈Z时,函数f(x)取最小值-2.
点评 本题考查三角函数化简求值,涉及三角函数的单调性和最值以及周期性,属基础题.

练习册系列答案
相关题目
14.已知椭圆$\frac{{x}^{2}}{4}$+y2=1的一个焦点坐标是( )
| A. | (2,1) | B. | (1,2) | C. | (0,$\sqrt{3}$) | D. | ($\sqrt{3}$,0) |
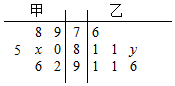 高三年级从甲(文)、乙(理)两个科组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩的茎叶图如图所示,其中甲组学生的平均分是85,乙组学生成绩的中位数是83.
高三年级从甲(文)、乙(理)两个科组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩的茎叶图如图所示,其中甲组学生的平均分是85,乙组学生成绩的中位数是83.