题目内容
4.已知△ABC,P为三角形所在平面上的一点,且点P满足:a$•\overrightarrow{PA}$+b$•\overrightarrow{PB}$+c$•\overrightarrow{PC}$=0,则P点为三角形( )| A. | 外心 | B. | 内心 | C. | 重心 | D. | 垂心 |
分析 在AB,AC上分别取单位向量$\overrightarrow{AD},\overrightarrow{AE}$,作$\overrightarrow{AF}=\overrightarrow{AD}+\overrightarrow{AE}$,则AF平分∠BAC,用$\overrightarrow{PA},\overrightarrow{AB},\overrightarrow{AC}$表示出$\overrightarrow{PB},\overrightarrow{PC}$代入条件式,用$\overrightarrow{AB},\overrightarrow{AC}$表示出$\overrightarrow{AP}$,则可证明A,F,P三点共线,即AP平分∠BAC.
解答 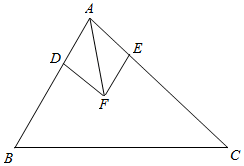 解在AB,AC上分别取点D,E,使得$\overrightarrow{AD}$=$\frac{\overrightarrow{AB}}{c}$,$\overrightarrow{AE}=\frac{\overrightarrow{AC}}{b}$,则$|\overrightarrow{AD}|=|\overrightarrow{AE}|$=1.
解在AB,AC上分别取点D,E,使得$\overrightarrow{AD}$=$\frac{\overrightarrow{AB}}{c}$,$\overrightarrow{AE}=\frac{\overrightarrow{AC}}{b}$,则$|\overrightarrow{AD}|=|\overrightarrow{AE}|$=1.
以AD,AE为邻边作平行四边形ADFE,则四边形ADFE是菱形,且$\overrightarrow{AF}$=$\overrightarrow{AD}+\overrightarrow{AE}$=$\frac{\overrightarrow{AB}}{c}+\frac{\overrightarrow{AC}}{b}$.
∴AF为∠BAC的平分线.
∵a$•\overrightarrow{PA}$+b$•\overrightarrow{PB}$+c$•\overrightarrow{PC}$=$\overrightarrow{0}$
∴a$•\overrightarrow{PA}$+b•($\overrightarrow{PA}+\overrightarrow{AB}$)+c•($\overrightarrow{PA}+\overrightarrow{AC}$)=$\overrightarrow{0}$,
即(a+b+c)$\overrightarrow{PA}$+b$\overrightarrow{AB}$+c$\overrightarrow{AC}$=$\overrightarrow{0}$,
∴$\overrightarrow{AP}$=$\frac{b}{a+b+c}\overrightarrow{AB}+\frac{c}{a+b+c}\overrightarrow{AC}$=$\frac{bc}{a+b+c}$($\frac{\overrightarrow{AB}}{c}+\frac{\overrightarrow{AC}}{b}$)=$\frac{bc}{a+b+c}$$\overrightarrow{AF}$.
∴A,P,F三点共线,即P在∠BAC的平分线上.
同理可得P在其他两角的平分线上,
∴P是△ABC的内心.
故选:B.
点评 本题考查了三角形内心的向量表示,向量的线性运算,属于中档题.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案| A. | 命题“p∨q”为真命题,则命题“p”和命题“q”均为真命题 | |
| B. | 已知x∈R,则“x>1”是“x>2”的充分不必要条件 | |
| C. | 命题“?x∈R,x2-x>0”的否定是:“?x∈R,x2-x≤0” | |
| D. | 命题“若am2<bm2,则a<b”的逆命题是真命题 |
| A. | 11 | B. | 12 | C. | 45 | D. | 120 |