题目内容
2.运行如图所示的流程图,则输出的结果S是$\frac{1}{2}$.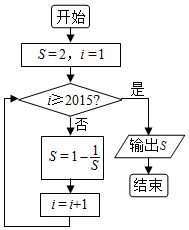
分析 变量i的值分别取1,2,3,4,…时,变量S的值依次为$\frac{1}{2}$,-1,2,$\frac{1}{2}$…,从而变量S的值是以3为周期在变化,由此可得结论.
解答 解:模拟执行程序,可得
S=2,i=1
不满足条件i≥2015,执行循环体,S=$\frac{1}{2}$,i=2
不满足条件i≥2015,执行循环体,S=-1,i=3
不满足条件i≥2015,执行循环体,S=2,i=4
…
观察规律可知,变量S的值是以3为周期在变化,
由于:2014=671×3+1,从而,有
i=2014,不满足条件i≥2015,执行循环体,S=$\frac{1}{2}$,i=2015
满足条件i≥2015,退出循环,输出S的值为$\frac{1}{2}$
故答案为:$\frac{1}{2}$.
点评 本题考查循环结构,考查学生的读图能力,属于基础题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
12.“p∨q为真”是“¬p为假”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
13.设F1,F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右两个焦点,若双曲线右支上存在一点P,使($\overrightarrow{OP}$+$\overrightarrow{O{F}_{2}}$)•($\overrightarrow{OP}$-$\overrightarrow{O{F}_{2}}$)=0(O为坐标原点),且|PF1|=$\sqrt{2}$|PF2|,则双曲线的离心率为( )
| A. | $\frac{\sqrt{3}+2}{2}$ | B. | $\sqrt{3}$+2 | C. | $\frac{\sqrt{3}+\sqrt{6}}{2}$ | D. | $\sqrt{3}$+$\sqrt{6}$ |
10.曲线y=x2与x=1及坐标轴围成的封闭区域为Ω1,不等式组$\left\{\begin{array}{l}{0≤x≤1}\\{0≤y≤1}\end{array}\right.$表示的平面区域为Ω2,在区域Ω2内随机取一点,则该点是取自于区域Ω1的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{5}$ |
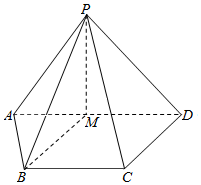 如图,在四棱锥P-ABCD中,AD∥BC,且AD=2BC,AD⊥CD,PA=PD,M为棱AD的中点.
如图,在四棱锥P-ABCD中,AD∥BC,且AD=2BC,AD⊥CD,PA=PD,M为棱AD的中点. 已知函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示;
已知函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示;