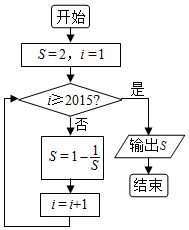
题目内容
7.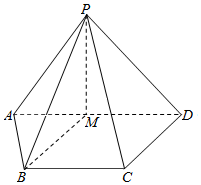 如图,在四棱锥P-ABCD中,AD∥BC,且AD=2BC,AD⊥CD,PA=PD,M为棱AD的中点.
如图,在四棱锥P-ABCD中,AD∥BC,且AD=2BC,AD⊥CD,PA=PD,M为棱AD的中点.(1)求证:CD∥平面PBM;
(2)求证:平面PAD⊥平面PBM.
分析 (1)证明四边形BCDM为平行四边形,可得CD∥BM,利用线面平行的判定定理证明CD∥平面PBM;
(2)利用线面垂直的判定定理证明AD⊥平面PBM,再证明平面PAD⊥平面PBM即可.
解答 证明:(1)因为AD∥BC,且AD=2BC,
所以四边形BCDM为平行四边形,
故CD∥BM,
又CD?平面PBM,BM?平面PBM,
所以CD∥平面PBM;(6分)
(2)因为PA=PD,点M为棱AD的中点,
所以PM⊥AD,
又AD⊥CD,CD∥BM,故AD⊥BM,
而PM∩BM=M,PM、BM?平面PBM,
所以AD⊥平面PBM,
又AD?平面PAD,所以平面PAD⊥平面PBM.(14分)
点评 本题考查线面平行、垂直的判定,考查平面与平面垂直,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.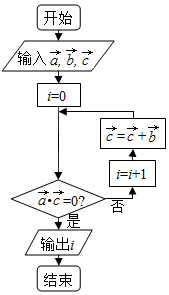 已知$\overrightarrow{a}$=$\overrightarrow{c}$=(-3,3),$\overrightarrow{b}$=(1,0),执行如图所示的程序框图,则输出i的值为( )
已知$\overrightarrow{a}$=$\overrightarrow{c}$=(-3,3),$\overrightarrow{b}$=(1,0),执行如图所示的程序框图,则输出i的值为( )
 已知$\overrightarrow{a}$=$\overrightarrow{c}$=(-3,3),$\overrightarrow{b}$=(1,0),执行如图所示的程序框图,则输出i的值为( )
已知$\overrightarrow{a}$=$\overrightarrow{c}$=(-3,3),$\overrightarrow{b}$=(1,0),执行如图所示的程序框图,则输出i的值为( )| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
15.“函数f(x)=kx-3在[-1,1]上有零点”是“k≥3”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 既不充分也不必要条件 | D. | 充要条件 |
12.已知函数f(x)=$\frac{asinx+3(x+2)^{2}}{{x}^{2}+4}$(a是不为0的常数),当x∈[-2,2]时,函数f(x)的最大值与最小值的和为( )
| A. | a+3 | B. | 6 | C. | 2 | D. | 3-a |
17.先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1,2,3,4,5,6),骰子朝上的面的点数分别为x,y,则log3(x+2y)=2的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |