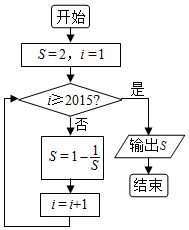
题目内容
14. 已知函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示;
已知函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示;(1)求ω,φ;
(2)将y=f(x)的图象向左平移θ(θ>0)个单位长度,得到y=g(x)的图象,若y=g(x)图象的一个对称点为($\frac{π}{3}$,0),求θ的最小值.
(3)对任意的x∈[$\frac{π}{4}$,$\frac{5π}{6}$]时,方程f(x)=m有两个不等根,求m的取值范围.
分析 (1)用五点法做函数y=Asin(ωx+φ)在一个周期上的简图.
(2)利用y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,求得θ的最小正值.
(3)利用正弦函数的定义域和值域,结合函数f(x)的图象,求得m的取值范围.
解答 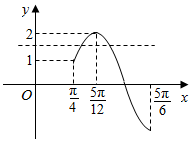 解:(1)根据函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象,可得$\frac{3}{4}$•$\frac{2π}{ω}$=$\frac{5π}{12}-(-\frac{π}{3})$,
解:(1)根据函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象,可得$\frac{3}{4}$•$\frac{2π}{ω}$=$\frac{5π}{12}-(-\frac{π}{3})$,
求得ω=2.
再根据五点法作图可得2•$\frac{5π}{12}$+φ=$\frac{π}{2}$,求得φ=-$\frac{π}{3}$,∴f(x)=2sin(2x-$\frac{π}{3}$).
(2)将y=f(x)的图象向左平移θ(θ>0)个单位长度,得到y=g(x)=2sin[2(x+θ)-$\frac{π}{3}$]=2sin(2x+2θ-$\frac{π}{3}$)的图象,
∵y=g(x)图象的一个对称点为($\frac{π}{3}$,0),∴2•$\frac{π}{3}$+2θ-$\frac{π}{3}$=kπ,k∈Z,∴θ=$\frac{kπ}{2}$-$\frac{π}{6}$,故θ的最小正值为$\frac{π}{3}$.
(3)对任意的x∈[$\frac{π}{4}$,$\frac{5π}{6}$]时,2x-$\frac{π}{3}$∈[$\frac{π}{6}$,$\frac{4π}{3}$],sin(2x-$\frac{π}{3}$)∈[-$\frac{\sqrt{3}}{2}$,1],即f(x)∈[-$\sqrt{3}$,2],
∵方程f(x)=m有两个不等根,结合函数f(x),x∈[$\frac{π}{4}$,$\frac{5π}{6}$]时的图象可得,1≤m<2.
点评 本题主要考查用五点法做函数y=Asin(ωx+φ)在一个周期上的简图,y=Asin(ωx+φ)的图象变换规律,正弦函数的定义域和值域,属于中档题.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案| A. | 1 | B. | 2 | C. | 3 | D. | $\sqrt{2}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $2\sqrt{2}$ | B. | 4 | C. | $±2\sqrt{2}$ | D. | ±4 |