题目内容
命题“存在实数x,使x2+2x-8=0”的否定是( )
| A、对任意实数x,都有x2+2x-8=0 |
| B、不存在实数x,使x2+2x-8≠0 |
| C、对任意实数x,都有x2+2x-8≠0 |
| D、存在实数x,使x2+2x-8≠0 |
考点:特称命题,命题的否定
专题:简易逻辑
分析:根据特称命题的否定是全称命题即可得到结论.
解答:
解:∵特称命题的否定是全称命题,
∴命题“存在实数x,使x2+2x-8=0”的否定是对任意实数x,都有x2+2x-8≠0,
故选:C
∴命题“存在实数x,使x2+2x-8=0”的否定是对任意实数x,都有x2+2x-8≠0,
故选:C
点评:本题主要考查含有量词的命题的否定,比较基础.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
设a>1>b>-1,则下列不等式一定成立的是( )
| A、a>b2 | ||||
| B、a2>2b | ||||
C、
| ||||
| D、|a|<|b| |
若
为任一非零向量,
为长度为1的向量,下列各式正确的是( )
| a |
| b |
A、|
| ||||
B、
| ||||
C、|
| ||||
D、|
|
下列函数满足|x|≥|f(x)|的是( )
| A、f(x)=ex-1 |
| B、f(x)=ln(x+1) |
| C、f(x)=tanx |
| D、f(x)=sinx |
设复数z+i(z为复数)在映射f下的象为zi,则-2+2i的象是( )
| A、2-2i | B、-2-2i |
| C、1-2i | D、-1-2i |
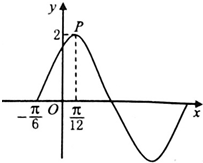 已知函数f(x)=2sin(ωx+φ),(ω>0,φ∈(0,
已知函数f(x)=2sin(ωx+φ),(ω>0,φ∈(0,