题目内容
假设数列{an}各项均不相等,将数列从小到大重新排序后相应的项数构成的新数列成为数列{an}的排序数列,例如:数列a2<a3<a1,满足则排序数列为2,3,1.
(1)写出2,4,3,1的排序数列;
(2)求证:数列{an}的排序数列为等差数列的充要条件是数列{an}为单调数列.
(1)写出2,4,3,1的排序数列;
(2)求证:数列{an}的排序数列为等差数列的充要条件是数列{an}为单调数列.
考点:数列的函数特性
专题:等差数列与等比数列
分析:(1)根据排序数列的定义,即可写出2,4,3,1的排序数列;
(2)根据等差数列的定义以及充要条件的定义即可证明数列{an}的排序数列为等差数列的充要条件是数列{an}为单调数列.
(2)根据等差数列的定义以及充要条件的定义即可证明数列{an}的排序数列为等差数列的充要条件是数列{an}为单调数列.
解答:
解:(Ⅰ)排序数列为4,1,3,2.
(Ⅱ)证明:充分性:D
当数列{an}单调增时,∵a1<a2<…<an,
∴排序数列为1,2,3,…,n.
∴排序数列为等差数列.
当数列{an}单调减时,∵an<an-1<…<a1,
∴排序数列为n,n-1,n-2,…,1.
∴排序数列为等差数列.
综上,数列{an}为单调数列时,排序数列为等差数列.
必要性:
∵排序数列为等差数列
∴排序数列为1,2,3,…,n或n,n-1,n-2,…,1.
∴a1<a2<…<an或an<an-1<…<a1,
∴数列{an}为单调数列.
(Ⅱ)证明:充分性:D
当数列{an}单调增时,∵a1<a2<…<an,
∴排序数列为1,2,3,…,n.
∴排序数列为等差数列.
当数列{an}单调减时,∵an<an-1<…<a1,
∴排序数列为n,n-1,n-2,…,1.
∴排序数列为等差数列.
综上,数列{an}为单调数列时,排序数列为等差数列.
必要性:
∵排序数列为等差数列
∴排序数列为1,2,3,…,n或n,n-1,n-2,…,1.
∴a1<a2<…<an或an<an-1<…<a1,
∴数列{an}为单调数列.
点评:本题主要考查等差数列充要条件的判断,考查学生的推理能力.

练习册系列答案
相关题目
在△ABC中,a,b,c分别为角A,B,C的对边,cos2
=
+
,则△ABC的形状为( )
| A |
| 2 |
| 1 |
| 2 |
| b |
| 2c |
| A、正三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰三角形 |
命题“存在实数x,使x2+2x-8=0”的否定是( )
| A、对任意实数x,都有x2+2x-8=0 |
| B、不存在实数x,使x2+2x-8≠0 |
| C、对任意实数x,都有x2+2x-8≠0 |
| D、存在实数x,使x2+2x-8≠0 |
已知A(2,2)、B(-1,3),若直线l过点P(1,1)且与线段AB相交,则直线l的倾斜角α的取值范围是( )
A、α≥
| ||||||||
B、
| ||||||||
| C、-1≤α≤1 | ||||||||
D、
|
直线2mx-(m2+1)y-
=0倾斜角的取值范围( )
| m |
| A、[0,π) | ||||
B、[0,
| ||||
C、[0,
| ||||
D、[0,
|
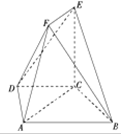 如图所示的几何体,四边形ABCD中,有AB∥CD,∠BAC=30°,AB=2CD=2,CB=1.点E在平面ABCD内的射影是点C,EF∥AC,且AC=2EF.
如图所示的几何体,四边形ABCD中,有AB∥CD,∠BAC=30°,AB=2CD=2,CB=1.点E在平面ABCD内的射影是点C,EF∥AC,且AC=2EF.