题目内容
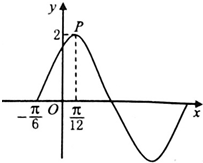已知函数f（x）=2sin（ωx+φ），（ω＞0，φ∈（0，| π |
| 2 |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
考点：由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质
分析：由图象求得四分之一周期，进一步求得周期，代入周期公式求得ω，再由五点作图的第一点求得φ，则函数解析式可求，（0）可求．
解答：
解：由三角函数的图象可知：
=
-(-
)=
．
∴T=π，则ω=
=
=2．
由五点作图的第一点可知：2×(-
)+φ=0，得φ=
，
∴f（x）=2sin（2x+
），
∴f（0）=2sin
=2×
=
．
故选：A．
| T |
| 4 |
| π |
| 12 |
| π |
| 6 |
| π |
| 4 |
∴T=π，则ω=
| 2π |
| T |
| 2π |
| π |
由五点作图的第一点可知：2×(-
| π |
| 6 |
| π |
| 3 |
∴f（x）=2sin（2x+
| π |
| 3 |
∴f（0）=2sin
| π |
| 3 |
| ||
| 2 |
| 3 |
故选：A．
点评：本题考查由y=Asin（ωx+φ）的部分图象求函数解析式，关键是由五点作图的某一点求φ，是中档题．
练习册系列答案
名校课堂系列答案
相关题目
在△ABC中，a，b，c分别为角A，B，C的对边，cos2
=
+
，则△ABC的形状为（ ）
| A |
| 2 |
| 1 |
| 2 |
| b |
| 2c |
| A、正三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰三角形 |
将“新、五、河”填入如图所示的4×4小方格内，每格内只填入一个汉字，且任意两个汉字既不同行也不同列，则不同的填写方法有（ ）| A、288 | B、144 |
| C、576 | D、96 |
复数
的实部是（ ）
| 1+i |
| 1-i |
| A、-2 | B、-1 | C、0 | D、1 |
复数z=
，则|z|=（ ）
| 1+i |
| i |
A、
| ||||
| B、2 | ||||
| C、1 | ||||
D、
|
命题“存在实数x，使x2+2x-8=0”的否定是（ ）
| A、对任意实数x，都有x2+2x-8=0 |
| B、不存在实数x，使x2+2x-8≠0 |
| C、对任意实数x，都有x2+2x-8≠0 |
| D、存在实数x，使x2+2x-8≠0 |