题目内容
某工业城市按照“十二五”(2011年至2015年)期间本地区主要污染物排放总量控制要求,进行减排治污.现以降低SO2的年排放量为例,原计划“十二五”期间每年的排放量都比上一年减少0.3万吨,已知该城市2011年SO2的年排放量约为9.3万吨,
(Ⅰ)按原计划,“十二五”期间该城市共排放SO2约多少万吨?
(Ⅱ)该城市为响应“十八大”提出的建设“美丽中国”的号召,决定加大减排力度.在2012年刚好按原计划完成减排任务的条件下,自2013年起,SO2的年排放量每年比上一年减少的百分率为p,为使2020年这一年的SO2年排放量控制在6万吨以内,求p的取值范围.
(参考数据
≈0.9505,
≈0.9559).
(Ⅰ)按原计划,“十二五”期间该城市共排放SO2约多少万吨?
(Ⅱ)该城市为响应“十八大”提出的建设“美丽中国”的号召,决定加大减排力度.在2012年刚好按原计划完成减排任务的条件下,自2013年起,SO2的年排放量每年比上一年减少的百分率为p,为使2020年这一年的SO2年排放量控制在6万吨以内,求p的取值范围.
(参考数据
| 8 |
| ||
| 9 |
| ||
考点:函数模型的选择与应用
专题:应用题,等差数列与等比数列
分析:(Ⅰ)确定2011年至2015年SO2的年排放量构成首项为9.3,公差为-0.3的等差数列,利用等差数列的求和公式,即可求得结论;
(Ⅱ)确定2012年至2020年SO2的年排放量构成首项为9,公比为1-p的等比数列,可得9×(1-p)8<6,即可求出结论.
(Ⅱ)确定2012年至2020年SO2的年排放量构成首项为9,公比为1-p的等比数列,可得9×(1-p)8<6,即可求出结论.
解答:
解:(Ⅰ)设“十二五”期间,该城市共排放SO2约y万吨,
依题意,2011年至2015年SO2的年排放量构成首项为9.3,公差为-0.3的等差数列,…(3分)
所以y=5×9.3+
×(-0.3)=43.5(万吨).
所以按计划“十二五”期间该城市共排放SO2约43.5万吨.…(6分)
(Ⅱ)由已知得,2012年的SO2年排放量9.6-0.3×2=9(万吨),…(7分)
所以2012年至2020年SO2的年排放量构成首项为9,公比为1-p的等比数列,…(9分)
由题意得9×(1-p)8<6,即1-p<
,
所以1-p<0.9505,解得p>4.95%.
所以SO2的年排放量每年减少的百分率p的取值范围4.95%<p<1…(12分)
依题意,2011年至2015年SO2的年排放量构成首项为9.3,公差为-0.3的等差数列,…(3分)
所以y=5×9.3+
| 5×(5-1) |
| 2 |
所以按计划“十二五”期间该城市共排放SO2约43.5万吨.…(6分)
(Ⅱ)由已知得,2012年的SO2年排放量9.6-0.3×2=9(万吨),…(7分)
所以2012年至2020年SO2的年排放量构成首项为9,公比为1-p的等比数列,…(9分)
由题意得9×(1-p)8<6,即1-p<
| 8 |
| ||
所以1-p<0.9505,解得p>4.95%.
所以SO2的年排放量每年减少的百分率p的取值范围4.95%<p<1…(12分)
点评:本小题主要考查等差数列、等比数列等基础知识,考查运算求解能力和应用意识,考查函数与方程思想.

练习册系列答案
相关题目
(理)下列函数中,在其定义域上不是奇函数的是( )
A、y=ln(x+
| ||||||||||
B、y=x(
| ||||||||||
C、y=ln|
| ||||||||||
| D、y=ln(secx+tanx) |
在平面直角坐标系中,记抛物线y=x-x2与x轴所围成的平面区域为M,该抛物线与直线y=kx(k>0)所围成的平面区域为A,向区域M内随机抛掷一点P,若点P落在区域A内的概率为
,则k的值为( )
| 8 |
| 27 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知i为虚数单位,a∈R,如果复数2i-
是实数,则a的值为( )
| a |
| 1-i |
| A、-4 | B、2 | C、-2 | D、4 |
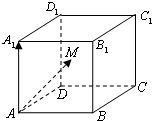 如图所示,在棱长为2的正方体ABCD-A1B1C1D1内(含正方体表面)任取一点M,则
如图所示,在棱长为2的正方体ABCD-A1B1C1D1内(含正方体表面)任取一点M,则| AA1 |
| AM |
A、
| ||
B、
| ||
C、
| ||
D、
|