题目内容
已知各项均为正数的数列{an}中,a1=1,Sn为数列{an}的前n项和.
(Ⅰ)若数列{an},{an2}都是等差数列,求数列{an}的通项公式;
(Ⅱ)若2Sn=an2+an,试比较
+
+…+
与1的大小.
(Ⅰ)若数列{an},{an2}都是等差数列,求数列{an}的通项公式;
(Ⅱ)若2Sn=an2+an,试比较
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| anan+1 |
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:(Ⅰ)设数列{an}的公差为d,由已知条件得到2a22=a12+a32,由此能求出d=0,从而得到an=1.
(Ⅱ)由2Sn=an2+an,得2Sn-1=an-12+an-1,二者相减能够推导出an=n,由此利用裂项相减法能比较
+
+…+
与1的大小.
(Ⅱ)由2Sn=an2+an,得2Sn-1=an-12+an-1,二者相减能够推导出an=n,由此利用裂项相减法能比较
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| anan+1 |
解答:
解:(Ⅰ)∵数列{an},{an2}都是等差数列,设数列{an}的公差为d,
∴2a22=a12+a32,∴2(a1+d)2=a12+(a1+2d)2,
∵a1=1,∴2(1+d)2=1+(1+2d)2,
整理,得2d2=0,∴d=0,∴an=1.…5分
(Ⅱ)由于2Sn=an2+an①
当n≥2时,2Sn-1=an-12+an-1②
由①-②得:an+an-1=
-an-12,
又an>0∴an-an-1=1 (n≥2,n∈N*),…10分
又a1=1,∴an=n;
∴
+
+…+
=
+
+…+
=(1-
)+(
-
)+…+(
-
)
=1-
<1.…13分.
∴2a22=a12+a32,∴2(a1+d)2=a12+(a1+2d)2,
∵a1=1,∴2(1+d)2=1+(1+2d)2,
整理,得2d2=0,∴d=0,∴an=1.…5分
(Ⅱ)由于2Sn=an2+an①
当n≥2时,2Sn-1=an-12+an-1②
由①-②得:an+an-1=
| a | 2 n |
又an>0∴an-an-1=1 (n≥2,n∈N*),…10分
又a1=1,∴an=n;
∴
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| anan+1 |
=
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| n(n+1) |
=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
点评:本题考查数列的通项公式的求法,考查两个数的大小的比较,是中档题,解题时要注意等差数列的通项公式、裂项求和的合理运用.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
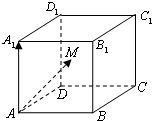 如图所示,在棱长为2的正方体ABCD-A1B1C1D1内(含正方体表面)任取一点M,则
如图所示,在棱长为2的正方体ABCD-A1B1C1D1内(含正方体表面)任取一点M,则| AA1 |
| AM |
A、
| ||
B、
| ||
C、
| ||
D、
|
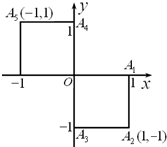 甲、乙、丙三人中要选一人去参加唱歌比赛,于是他们制定了一个规则,规则为:(如图)以O为起点,再从A1,A2,A3,A4,A5,这5个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若X>0就让甲去;若X=0就让乙去;若X<0就是丙去.
甲、乙、丙三人中要选一人去参加唱歌比赛,于是他们制定了一个规则,规则为:(如图)以O为起点,再从A1,A2,A3,A4,A5,这5个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若X>0就让甲去;若X=0就让乙去;若X<0就是丙去.