题目内容
在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系.已知直线l的参数方程为
(t为参数),圆C的极坐标方程为ρ=2
cos(θ-
).
(Ⅰ)若圆C关于直线l对称,求a的值;
(Ⅱ)若圆C与直线l相切,求a的值.
|
| 2 |
| π |
| 4 |
(Ⅰ)若圆C关于直线l对称,求a的值;
(Ⅱ)若圆C与直线l相切,求a的值.
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:(I)把直线l的参数方程和圆C的极坐标方程分别化为直角坐标方程,再利用圆C关于直线l对称可得直线l过圆心,即可得出.
(II)利用圆C与直线l相切?点C到直线l的距离d=r,即可得出.
(II)利用圆C与直线l相切?点C到直线l的距离d=r,即可得出.
解答:
解:(Ⅰ)由直线l的参数方程为
(t为参数)消去参数t可得:直线l:x+ay+a-5=0;
由圆C的极坐标方程为ρ=2
cos(θ-
),化为ρ2=2ρcosθ+2ρsinθ,
∴x2+y2-2x-2y=0,即(x-1)2+(y-1)2=2.
∴圆心为C(1,1),半径r=
.
∵圆C关于直线l对称,∴直线l过圆心,
∴1+a•1+a-5=0,
解得a=2;
(Ⅱ)点C到直线l的距离d=
,
∵圆C与直线l相切,∴d=r.
∴
=
,
整理得a2-8a+7=0,
解得a=1或a=7.
|
由圆C的极坐标方程为ρ=2
| 2 |
| π |
| 4 |
∴x2+y2-2x-2y=0,即(x-1)2+(y-1)2=2.
∴圆心为C(1,1),半径r=
| 2 |
∵圆C关于直线l对称,∴直线l过圆心,
∴1+a•1+a-5=0,
解得a=2;
(Ⅱ)点C到直线l的距离d=
| 2|a-2| | ||
|
∵圆C与直线l相切,∴d=r.
∴
| 2|a-2| | ||
|
| 2 |
整理得a2-8a+7=0,
解得a=1或a=7.
点评:本题考查了把直线l的参数方程和圆C的极坐标方程分别化为直角坐标方程、圆的对称性质、圆C与直线l相切?点C到直线l的距离d=r等基础知识与基本技能方法,属于基础题.

练习册系列答案
相关题目
“函数f(x)=x2+2x+m存在零点”的一个必要不充分条件是( )
| A、m≤1 | B、m≤2 |
| C、m≤0 | D、1≤m≤2 |
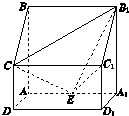 如图所示,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
如图所示,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.