题目内容
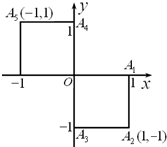 甲、乙、丙三人中要选一人去参加唱歌比赛,于是他们制定了一个规则,规则为:(如图)以O为起点,再从A1,A2,A3,A4,A5,这5个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若X>0就让甲去;若X=0就让乙去;若X<0就是丙去.
甲、乙、丙三人中要选一人去参加唱歌比赛,于是他们制定了一个规则,规则为:(如图)以O为起点,再从A1,A2,A3,A4,A5,这5个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若X>0就让甲去;若X=0就让乙去;若X<0就是丙去.(Ⅰ)写出数量积X的所有可能取值;
(Ⅱ)求甲、乙、丙三人去参加比赛的概率,并由求出的概率来说明这个规则公平吗?
考点:古典概型及其概率计算公式,平面向量数量积的运算
专题:平面向量及应用,概率与统计
分析:(Ⅰ)根据向量数量积的定义即可计算X的所有可能取值;
(Ⅱ)
(Ⅱ)
解答:
解:(Ⅰ)由题意可得:
•
=(1,0)•(1,-1)=1,
•
=(1,0)•(0,-1)=0,
•
=(1,0)•(0,1)=0,
•
=(1,0)•(-1,1)=-1,
•
=(1,-1)•(0,-1)=1,
•
=(1,-1)•(0,1)=-1,
•
=(1,-1)•(-1,1)=-2,
•
=(0,-1)•(0,1)=-1,
•
=(0,-1)•(-1,1)=-1,
•
=(0,1)•(-1,1)=1.
∴X的所有可能取值为-2,-1,0,1.
(Ⅱ)由(Ⅰ)可知基本事件共10个,
X>0的事件有3个,
X=0的事件有2个,
X<0的事件有5个,
P(甲去)=
.
P(乙去)=
.
P(丙去)=
.
甲乙丙去的概率不相同,
∴这个规则不公平.
| OA1 |
| OA2 |
| OA1 |
| OA3 |
| OA1 |
| OA4 |
| OA1 |
| OA5 |
| OA2 |
| OA3 |
| OA2 |
| OA4 |
| OA2 |
| OA5 |
| OA3 |
| OA4 |
| OA3 |
| OA5 |
| OA4 |
| OA5 |
∴X的所有可能取值为-2,-1,0,1.
(Ⅱ)由(Ⅰ)可知基本事件共10个,
X>0的事件有3个,
X=0的事件有2个,
X<0的事件有5个,
P(甲去)=
| 3 |
| 10 |
P(乙去)=
| 2 |
| 10 |
P(丙去)=
| 5 |
| 10 |
甲乙丙去的概率不相同,
∴这个规则不公平.
点评:本题考查古典概型及其概率公式,以及平面向量的数量积的运算的综合应用,属中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
函数f(x)=
在[2,+∞)上为增函数,且f(0)=0,则f(x)的最小值是( )
|
|
| A、f(2) | B、f(0) |
| C、f(-2) | D、f(4) |
已知实数x、y满足约束条件
,若
=(x,y),
=(3,-1),设z表示向量
在
方向上的投影,则z的取值范围是( )
|
| a |
| b |
| a |
| b |
A、[-
| ||||||||
| B、[-1,6] | ||||||||
C、[-
| ||||||||
D、[-
|
“函数f(x)=x2+2x+m存在零点”的一个必要不充分条件是( )
| A、m≤1 | B、m≤2 |
| C、m≤0 | D、1≤m≤2 |
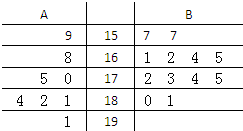 某园艺师培育了两种珍稀树苗A与B,株数分别为8与12,现将这20株树苗的高度编写成如图所示茎叶图(单位:cm).若树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售.
某园艺师培育了两种珍稀树苗A与B,株数分别为8与12,现将这20株树苗的高度编写成如图所示茎叶图(单位:cm).若树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售.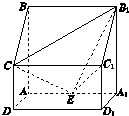 如图所示,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
如图所示,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.