题目内容
已知函数f(x)=x3+
x2+ax+b(a,b为常数),其图象是曲线C.
(1)当a=-2时,求函数f(x)的单调减区间;
(2)设函数f(x)的导函数为f′(x),若存在唯一的实数x0,使得f(x0)=x0与f′(x0)=0同时成立,求实数b的取值范围;
(3)已知点A为曲线C上的动点,在点A处作曲线C的切线l1与曲线C交于另一点B,在点B处作曲线C的切线l2,设切线l1,l2的斜率分别为k1,k2.问:是否存在常数λ,使得k2=λk1?若存在,求出λ的值;若不存在,请说明理由.
| 5 |
| 2 |
(1)当a=-2时,求函数f(x)的单调减区间;
(2)设函数f(x)的导函数为f′(x),若存在唯一的实数x0,使得f(x0)=x0与f′(x0)=0同时成立,求实数b的取值范围;
(3)已知点A为曲线C上的动点,在点A处作曲线C的切线l1与曲线C交于另一点B,在点B处作曲线C的切线l2,设切线l1,l2的斜率分别为k1,k2.问:是否存在常数λ,使得k2=λk1?若存在,求出λ的值;若不存在,请说明理由.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:压轴题,导数的综合应用
分析:(1)先求原函数的导数,根据f′(x)<0求得的区间是单调减区间,即可;
(2)由于存在唯一的实数x0,使得f(x0)=x0与f′(x0)=0同时成立,则
存在唯一的实数根x0,即b=2x3+
x2+x存在唯一的实数根x0,就把问题转化为求函数最值问题;
(3)假设存在常数λ,依据曲线C在点A处的切线l1与曲线C交于另一点B,曲线C在点B处的切线l2,得到关于λ的方程,有解则存在,无解则不存在.
(2)由于存在唯一的实数x0,使得f(x0)=x0与f′(x0)=0同时成立,则
|
| 5 |
| 2 |
(3)假设存在常数λ,依据曲线C在点A处的切线l1与曲线C交于另一点B,曲线C在点B处的切线l2,得到关于λ的方程,有解则存在,无解则不存在.
解答:
解:(1)当a=-2时,函数f(x)=x3+
x2-2x+b
则f′(x)=3x2+5x-2=(3x-1)(x+2)
令f′(x)<0,解得-2<x<
,
所以f(x)的单调递减区间为(-2,
);
(2)函数f(x)的导函数为由于存在唯一的实数x0,使得f(x0)=x0与f′(x0)=0同时成立,
则
即x3+
x2+(-3x2-5x-1)x+b=0存在唯一的实数根x0,
故b=2x3+
x2+x存在唯一的实数根x0,
令y=2x3+
x2+x,则y′=6x2+5x+1=(2x+1)(3x+1)=0,故x=-
或x=-
,
则函数y=2x3+
x2+x在(-∞,-
),(-
,+∞)上是增函数,在(-
,-
)上是减函数,
由于x=-
时,y=-
;x=-
时,y=-
;
故实数b的取值范围为:(-∞,-
)∪(-
,+∞);
(3)设点A(x0,f(x0)),则在点A处的切线l1的切线方程为y-f(x0)=f′(x0)(x-x0),
与曲线C联立得到f(x)-f(x0)=f′(x0)(x-x0),
即(x3+
x2+ax+b)-(x03+
x02+ax0+b)=(3x02+5x0+a)(x-x0),
整理得到(x-x0)2[x+(2x0+
)]=0,
故点B的横坐标为xB=-(2x0+
)
由题意知,切线l1的斜率为k1=f′(x0)=3x02+5x0+a,
l2的斜率为k2=f′(-(2x0+
))=12x02+20x0+
+a,
若存在常数λ,使得k2=λk1,则12x02+20x0+
+a=λ(3x02+5x0+a),
即存在常数λ,使得(4-λ)(3x02+5x0)=(λ-1)a-
,
故
,解得λ=4,a=
,
故a=
时,存在常数λ=4,使得k2=4k1;a≠
时,不存在常数,使得k2=4k1.
| 5 |
| 2 |
则f′(x)=3x2+5x-2=(3x-1)(x+2)
令f′(x)<0,解得-2<x<
| 1 |
| 3 |
所以f(x)的单调递减区间为(-2,
| 1 |
| 3 |
(2)函数f(x)的导函数为由于存在唯一的实数x0,使得f(x0)=x0与f′(x0)=0同时成立,
则
|
| 5 |
| 2 |
故b=2x3+
| 5 |
| 2 |
令y=2x3+
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
则函数y=2x3+
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
由于x=-
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 3 |
| 7 |
| 54 |
故实数b的取值范围为:(-∞,-
| 7 |
| 54 |
| 1 |
| 8 |
(3)设点A(x0,f(x0)),则在点A处的切线l1的切线方程为y-f(x0)=f′(x0)(x-x0),
与曲线C联立得到f(x)-f(x0)=f′(x0)(x-x0),
即(x3+
| 5 |
| 2 |
| 5 |
| 2 |
整理得到(x-x0)2[x+(2x0+
| 5 |
| 2 |
故点B的横坐标为xB=-(2x0+
| 5 |
| 2 |
由题意知,切线l1的斜率为k1=f′(x0)=3x02+5x0+a,
l2的斜率为k2=f′(-(2x0+
| 5 |
| 2 |
| 25 |
| 4 |
若存在常数λ,使得k2=λk1,则12x02+20x0+
| 25 |
| 4 |
即存在常数λ,使得(4-λ)(3x02+5x0)=(λ-1)a-
| 25 |
| 4 |
故
|
| 25 |
| 12 |
故a=
| 25 |
| 12 |
| 25 |
| 12 |
点评:本题以函数为载体,考查导数知识的运用,考查函数的单调性,考查曲线的切线,同时还考查了方程根的问题,一般要转化为函数的最值来解决.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
空间中一正方形的边长为3.一平面使得A、B、C、D四点到的距离都为1,则这样的平面有( )
| A、2个 | B、4个 | C、5个 | D、6个 |
已知∠BAC在平面α内,PA是α的斜线,若∠PAB=∠PAC=∠BAC=60°,PA=a,则点P到平面α的距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
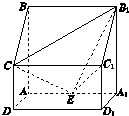 如图所示,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
如图所示,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.