题目内容
设α,β为不重合的平面,m,n为不重合的直线,则下列命题正确的是( )
| A、若α⊥β,α∩β=n,m⊥n,则m⊥α |
| B、若m?α,n?β,m⊥n,则n⊥α |
| C、若n⊥α,n⊥β,m⊥β,则m⊥α |
| D、若m∥α,n∥β,m⊥n,则α⊥β |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:利用线面、面面垂直的判定定理判断.
解答:
解:对于A,α⊥β,α∩β=m时,若n⊥m,n?α,则n⊥β,但题目中无条件n?α,故A也不一定成立;
对于B,由线面平行的判定,一条直线垂直于一个平面内的两条相交直线,则线面垂直,而选项B中,只有m⊥n,则n⊥α,显然不成立;
对于C,n⊥α,n⊥β,则α∥β,又m⊥β,则m⊥α,结论成立;
对于D,同由面面平行的判定,一个面经过另一个面的垂线,仅有m⊥n,不能得到m⊥β或n⊥α,故不正确.
故选C
对于B,由线面平行的判定,一条直线垂直于一个平面内的两条相交直线,则线面垂直,而选项B中,只有m⊥n,则n⊥α,显然不成立;
对于C,n⊥α,n⊥β,则α∥β,又m⊥β,则m⊥α,结论成立;
对于D,同由面面平行的判定,一个面经过另一个面的垂线,仅有m⊥n,不能得到m⊥β或n⊥α,故不正确.
故选C
点评:本题考查线面、面面垂直的判定定理的应用.

练习册系列答案
相关题目
已知点P(1,3)在直线
+
=1(a>0,b>0),则a+2b的最小值为( )
| x |
| a |
| y |
| b |
A、7+2
| ||
B、2
| ||
C、7+2
| ||
| D、14 |
已知sin(α+
)=-
,则cos(
-α)=( )
| π |
| 3 |
| 5 |
| 13 |
| π |
| 6 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
在复平面内,O是原点,复数2+i与-3+4i(i为虚数单位)对应的向量分别是
与
,则向量
对应的复数是( )
| OA |
| OB |
| AB |
| A、-1+5i | B、-5+3i |
| C、5-3i | D、5-i |
已知平面向量
=(2,1),且
∥
,则
可能是( )
| a |
| a |
| b |
| b |
| A、(1,-2) |
| B、(-4,-2) |
| C、(-1,-2) |
| D、(4,-2) |
命题“如果x≤2mn,那么x≤m2+n2”的逆否命题是( )
| A、如果x>2mn,那么x≥m2+n2 |
| B、如果x≥m2+n2,那么x≥2mn |
| C、如果x>m2+n2,那么x>2mn |
| D、如果x<2mn,那么x≤m2+n2 |
不等式x2+3x-4<0的解集为( )
| A、{x|x<-1,或x>4} |
| B、{x|-3<x<0} |
| C、{x|x<-4,或x>1} |
| D、{x|-4<x<1} |
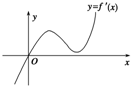 定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示.若两正数a,b满足f(2a+b)<1,则
定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示.若两正数a,b满足f(2a+b)<1,则