题目内容
20.已知向量$\overrightarrow{a}$=(sin2α-$\frac{2\sqrt{5}}{3}$,2cosα),$\overrightarrow{b}$=(1,1-sinα),α∈(0,π),且$\overrightarrow{a}$$⊥\overrightarrow{b}$,则tan($α-\frac{π}{4}$)=( )| A. | 9-4$\sqrt{5}$ | B. | 4$\sqrt{5}$-9 | C. | 5$\sqrt{2}$-9 | D. | 9+4$\sqrt{5}$ |
分析 由条件利用两个向量垂直的性质求得cosα 的值,可得sinα、tanα的值,再利用两角差的正切公式求得tan($α-\frac{π}{4}$)的值.
解答 解:由$\overrightarrow{a}$$⊥\overrightarrow{b}$,α∈(0,π),可得$\overrightarrow{a}•\overrightarrow{b}$=sin2α-$\frac{2\sqrt{5}}{3}$+2cosα(1-sinα)=2cosα-$\frac{2\sqrt{5}}{3}$=0,
∴cosα=$\frac{\sqrt{5}}{3}$,∴sinα=$\frac{2}{3}$,∴tanα=$\frac{sinα}{cosα}$=$\frac{2}{\sqrt{5}}$,
∴tan($α-\frac{π}{4}$)=$\frac{tanα-1}{1+tanα}$=4$\sqrt{5}$-9,
故选:B.
点评 本题主要考查两个向量垂直的性质,两角差的正切公式的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
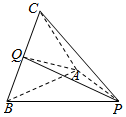 如图,在三棱锥P-ABC中,PA=PB=AB=BC=2,∠CBA=∠PBC=60°,Q为线段BC的中点.
如图,在三棱锥P-ABC中,PA=PB=AB=BC=2,∠CBA=∠PBC=60°,Q为线段BC的中点.