题目内容
5.n∈N*,A${\;}_{n}^{3}$+A${\;}_{4}^{n+1}$的值为30.分析 由题意得n=3,代入排列数公式,可得答案.
解答 解:由题意得:n≥3,且n+1≤4,即n=3,
∴A${\;}_{n}^{3}$+A${\;}_{4}^{n+1}$=${A}_{3}^{3}$+${A}_{4}^{4}$=6+24=30,
故答案为:30.
点评 本题考查的知识点是排列及排列数公式,根据已知得到n=3是解答的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
15.函数f(x)=$\frac{4-x}{4x-2}$,在区间(0,$\frac{1}{2}$)∪($\frac{1}{2}$,2)上函数f(x)≥1的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{7}{20}$ | C. | $\frac{9}{20}$ | D. | $\frac{1}{2}$ |
20.已知向量$\overrightarrow{a}$=(sin2α-$\frac{2\sqrt{5}}{3}$,2cosα),$\overrightarrow{b}$=(1,1-sinα),α∈(0,π),且$\overrightarrow{a}$$⊥\overrightarrow{b}$,则tan($α-\frac{π}{4}$)=( )
| A. | 9-4$\sqrt{5}$ | B. | 4$\sqrt{5}$-9 | C. | 5$\sqrt{2}$-9 | D. | 9+4$\sqrt{5}$ |
14.若实数x,y满足x2+y2-2x+2$\sqrt{3}$y+3=0,则x-$\sqrt{3}$y的取值范围是( )
| A. | [2,+∞) | B. | (2,6) | C. | [2,6] | D. | [-4,0] |
15.设向量$\overrightarrow{AB}$=(3,4),$\overrightarrow{BC}$=(-2,-1),则cos∠BAC等于( )
| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
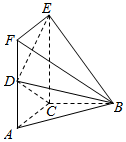 如图,矩形ACEF所在的平面与Rt△ABC所在的平面垂直,D是AF的中点,且AC=BC=AD=$\frac{1}{2}$CE.
如图,矩形ACEF所在的平面与Rt△ABC所在的平面垂直,D是AF的中点,且AC=BC=AD=$\frac{1}{2}$CE.