题目内容
15.已知眨tanα,tanβ是方程x2+3$\sqrt{3}$x+4=0的两根,且-$\frac{π}{2}$<α<$\frac{π}{2}$,-$\frac{π}{2}$$<β<\frac{π}{2}$,进一步准确判断α,β所在象限并求角α+β.分析 由条件利用韦达定理求得α、β为第四象限角;再结合tan(α+β)=$\sqrt{3}$,α+β∈(-π,0),可得α+β的值.
解答 解:由题意可得tanα+tanβ=-3$\sqrt{3}$,tanα•tanβ=4,再根据-$\frac{π}{2}$<α<$\frac{π}{2}$,-$\frac{π}{2}$$<β<\frac{π}{2}$,
可得α、β∈(-$\frac{π}{2}$,0),即α、β均为第四象限角.
再结合tan(α+β)=$\frac{tanα+tanβ}{1-tanα•tanβ}$=$\sqrt{3}$,α+β∈(-π,0),
可得α+β=-$\frac{2π}{3}$.
点评 本题主要考查韦达定理,两角和差的正切公式,属于基础题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
3.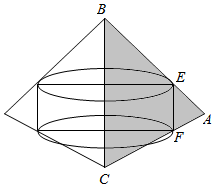 △ABC中,E,F分别为AB,AC的中点,以BC为边所在直线为轴旋转,四边形BCFE和△AEF旋转所得的几何体的体积分别为V1,V2,则( )
△ABC中,E,F分别为AB,AC的中点,以BC为边所在直线为轴旋转,四边形BCFE和△AEF旋转所得的几何体的体积分别为V1,V2,则( )
 △ABC中,E,F分别为AB,AC的中点,以BC为边所在直线为轴旋转,四边形BCFE和△AEF旋转所得的几何体的体积分别为V1,V2,则( )
△ABC中,E,F分别为AB,AC的中点,以BC为边所在直线为轴旋转,四边形BCFE和△AEF旋转所得的几何体的体积分别为V1,V2,则( )| A. | V1>V2 | B. | V1<V2 | ||
| C. | V1=V2 | D. | V1,V2大小关系不确定 |
20.已知向量$\overrightarrow{a}$=(sin2α-$\frac{2\sqrt{5}}{3}$,2cosα),$\overrightarrow{b}$=(1,1-sinα),α∈(0,π),且$\overrightarrow{a}$$⊥\overrightarrow{b}$,则tan($α-\frac{π}{4}$)=( )
| A. | 9-4$\sqrt{5}$ | B. | 4$\sqrt{5}$-9 | C. | 5$\sqrt{2}$-9 | D. | 9+4$\sqrt{5}$ |
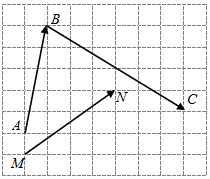 向量$\overrightarrow{AB}$,$\overrightarrow{BC}$,$\overrightarrow{MN}$在正方形网格中的位置如图所示,若$\overrightarrow{MN}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$(λ,μ∈R),则$\frac{λ}{μ}$=2.
向量$\overrightarrow{AB}$,$\overrightarrow{BC}$,$\overrightarrow{MN}$在正方形网格中的位置如图所示,若$\overrightarrow{MN}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$(λ,μ∈R),则$\frac{λ}{μ}$=2.