题目内容
11.若有点M1(4,3)和M2(2,-1),点M分有向线段$\overrightarrow{{{M}_{1}M}_{2}}$的比λ=-2.则点M的坐标(0,-5).分析 点M分有向线段$\overrightarrow{{{M}_{1}M}_{2}}$的比λ=-2.可得点M2是线段M1M的中点,利用中点坐标公式即可得出.
解答 解:∵点M分有向线段$\overrightarrow{{{M}_{1}M}_{2}}$的比λ=-2.
∴点M2是线段M1M的中点,
设M(x,y),
则$\left\{\begin{array}{l}{2=\frac{4+x}{2}}\\{-1=\frac{3+y}{2}}\end{array}\right.$,解得x=0,y=-5.
故答案为:(0,-5).
点评 本题考查了共线向量定理、中点坐标公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
1.设θ为第二象限角,若$tan(θ+\frac{π}{3})=\frac{1}{2}$,则sinθ+$\sqrt{3}$cosθ=( )
| A. | -1 | B. | 1 | C. | $-\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
19.某化工厂产生的废气经过过滤后排放,以模型$y={P_0}{e^{-kx}}$去拟合过滤过程中废气的污染物数量ymg/L与时间xh间的一组数据时,为了求出回归方程,设z=lny,其变换后得到线性回归方程z=-0.5x+2+ln300,则当经过6h后,预报废气的污染物数量为( )
| A. | 300e2mg/L | B. | 300emg/L | C. | $\frac{300}{e^2}$mg/L | D. | $\frac{300}{e}$mg/L |
3.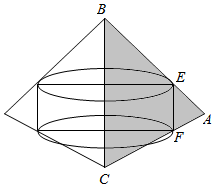 △ABC中,E,F分别为AB,AC的中点,以BC为边所在直线为轴旋转,四边形BCFE和△AEF旋转所得的几何体的体积分别为V1,V2,则( )
△ABC中,E,F分别为AB,AC的中点,以BC为边所在直线为轴旋转,四边形BCFE和△AEF旋转所得的几何体的体积分别为V1,V2,则( )
 △ABC中,E,F分别为AB,AC的中点,以BC为边所在直线为轴旋转,四边形BCFE和△AEF旋转所得的几何体的体积分别为V1,V2,则( )
△ABC中,E,F分别为AB,AC的中点,以BC为边所在直线为轴旋转,四边形BCFE和△AEF旋转所得的几何体的体积分别为V1,V2,则( )| A. | V1>V2 | B. | V1<V2 | ||
| C. | V1=V2 | D. | V1,V2大小关系不确定 |
20.已知向量$\overrightarrow{a}$=(sin2α-$\frac{2\sqrt{5}}{3}$,2cosα),$\overrightarrow{b}$=(1,1-sinα),α∈(0,π),且$\overrightarrow{a}$$⊥\overrightarrow{b}$,则tan($α-\frac{π}{4}$)=( )
| A. | 9-4$\sqrt{5}$ | B. | 4$\sqrt{5}$-9 | C. | 5$\sqrt{2}$-9 | D. | 9+4$\sqrt{5}$ |
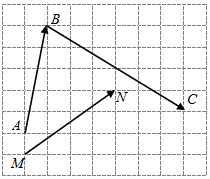 向量$\overrightarrow{AB}$,$\overrightarrow{BC}$,$\overrightarrow{MN}$在正方形网格中的位置如图所示,若$\overrightarrow{MN}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$(λ,μ∈R),则$\frac{λ}{μ}$=2.
向量$\overrightarrow{AB}$,$\overrightarrow{BC}$,$\overrightarrow{MN}$在正方形网格中的位置如图所示,若$\overrightarrow{MN}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$(λ,μ∈R),则$\frac{λ}{μ}$=2.