题目内容
10.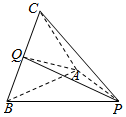 如图,在三棱锥P-ABC中,PA=PB=AB=BC=2,∠CBA=∠PBC=60°,Q为线段BC的中点.
如图,在三棱锥P-ABC中,PA=PB=AB=BC=2,∠CBA=∠PBC=60°,Q为线段BC的中点.(1)求证:PA⊥BC;
(2)求点Q到平面PAC的距离.
分析 (1)由题意得到三角形ABC为等边三角形,由Q为BC中点,得到AQ垂直于BC,同理得到三角形BPC为等边三角形,得到PQ垂直于BC,由AQ与QC交于Q,得到BC与平面APQ垂直,而AP属于平面PAQ,即可得到PA与BC垂直;
(2)设点Q到平面PAC的距离为h,根据VQ-ACP=VC-APQ,利用体积法求出h,即为点Q到平面PAC的距离.
解答 (1)证明:∵在△ABC中,BC=AB,∠CBA=60°,
∴△ABC为等边三角形,
∵Q为BC的中点,
∴AQ⊥BC,
同理在等边△BPC中,PQ⊥BC,
∵QA∩QC=Q,
∴BC⊥平面PAQ,
∵AP?平面PAQ,
∴BC⊥PA;
(2)设点Q到平面PAC的距离为h,由(1)得QA=QP=$\sqrt{3}$,
∵AP=2,
∴S△QPA=$\frac{1}{2}$×2×$\sqrt{2}$=$\sqrt{2}$,
∵BC⊥平面PAQ,且CQ=1,
∴VC-PAQ=$\frac{1}{3}$×$\sqrt{2}$×1=$\frac{\sqrt{2}}{3}$,
∵AC=AP=PC=2,
∴S△PAC=$\frac{1}{2}$×2×2×sin60°=$\sqrt{3}$,
∴VQ-PAC=$\frac{1}{3}$×$\sqrt{3}$×h,
∵VC-PAQ=VQ-PAC,
∴$\frac{\sqrt{2}}{3}$=$\frac{1}{3}$×$\sqrt{3}$×h,
解得:h=$\frac{\sqrt{6}}{3}$,
则点Q到平面PAC的距离为$\frac{\sqrt{6}}{3}$.
点评 此题考查了点、线、面之间的距离,等边三角形的判定与性质,以及直线与平面垂直的判定与性质,熟练掌握判定与性质是解本题的关键.

练习册系列答案
相关题目
1.设θ为第二象限角,若$tan(θ+\frac{π}{3})=\frac{1}{2}$,则sinθ+$\sqrt{3}$cosθ=( )
| A. | -1 | B. | 1 | C. | $-\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
15.函数f(x)=$\frac{4-x}{4x-2}$,在区间(0,$\frac{1}{2}$)∪($\frac{1}{2}$,2)上函数f(x)≥1的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{7}{20}$ | C. | $\frac{9}{20}$ | D. | $\frac{1}{2}$ |
19.某化工厂产生的废气经过过滤后排放,以模型$y={P_0}{e^{-kx}}$去拟合过滤过程中废气的污染物数量ymg/L与时间xh间的一组数据时,为了求出回归方程,设z=lny,其变换后得到线性回归方程z=-0.5x+2+ln300,则当经过6h后,预报废气的污染物数量为( )
| A. | 300e2mg/L | B. | 300emg/L | C. | $\frac{300}{e^2}$mg/L | D. | $\frac{300}{e}$mg/L |
20.已知向量$\overrightarrow{a}$=(sin2α-$\frac{2\sqrt{5}}{3}$,2cosα),$\overrightarrow{b}$=(1,1-sinα),α∈(0,π),且$\overrightarrow{a}$$⊥\overrightarrow{b}$,则tan($α-\frac{π}{4}$)=( )
| A. | 9-4$\sqrt{5}$ | B. | 4$\sqrt{5}$-9 | C. | 5$\sqrt{2}$-9 | D. | 9+4$\sqrt{5}$ |
 某商场举行购物抽奖活动,抽奖箱中放有除编号不同外,其余均相同的20个小球,这20个小球编号的茎叶图如图所示,活动规则如下:从抽奖箱中随机抽取一球,若抽取的小球编号是十位数字为l的奇数,则为一等奖,奖金100元;若抽取的小球编号是十位数字为2的奇数,则为二等奖,奖金50元;若抽取的小球是其余编号则不中奖.现某顾客有放回的抽奖两次,两次抽奖相互独立.
某商场举行购物抽奖活动,抽奖箱中放有除编号不同外,其余均相同的20个小球,这20个小球编号的茎叶图如图所示,活动规则如下:从抽奖箱中随机抽取一球,若抽取的小球编号是十位数字为l的奇数,则为一等奖,奖金100元;若抽取的小球编号是十位数字为2的奇数,则为二等奖,奖金50元;若抽取的小球是其余编号则不中奖.现某顾客有放回的抽奖两次,两次抽奖相互独立.