题目内容
若数列{an}为等差数列,且a1=1,a2+a3+a4=21,则
= .
| lim |
| n→∞ |
| a1+a2+…+an |
| n2 |
考点:等差数列的性质,极限及其运算
专题:等差数列与等比数列
分析:设出等差数列的公差,由已知求得公差,然后求等差数列的前n项和后代入
得答案.
| lim |
| n→∞ |
| a1+a2+…+an |
| n2 |
解答:
解:设等差数列{an}的公差为d,由a1=1,a2+a3+a4=21,得
3a1+6d=21,即3+6d=21,d=3.
∴
=
=
=
=
.
故答案为:
.
3a1+6d=21,即3+6d=21,d=3.
∴
| lim |
| n→∞ |
| a1+a2+…+an |
| n2 |
| lim |
| n→∞ |
n+
| ||
| n2 |
| lim |
| n→∞ |
| 3n-1 |
| 2n |
| lim |
| n→∞ |
3-
| ||
| 2 |
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题考查了等差数列的性质,考查了数列极限的求法,是基础题.

练习册系列答案
相关题目
已知数列{an}为等比数列,a5=1,a9=81,则a7=( )
| A、9或-9 | B、9 |
| C、27或-27 | D、-27 |
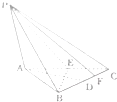 在三棱锥P-ABC中,底面ABC是边长为2的正三角形,PA⊥平面ABC,D,E分别为BC,AC的中点,F是CD的中点.
在三棱锥P-ABC中,底面ABC是边长为2的正三角形,PA⊥平面ABC,D,E分别为BC,AC的中点,F是CD的中点.