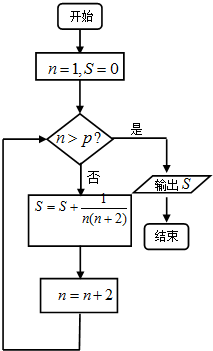
题目内容
菱形ABCD,边长为1,E为CD的中点,O为两对角线交点,则
•
的取值范围是 .
| OD |
| OE |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由题意可得则|
|=
,设∠DAO=θ,则 θ∈(0
),∠DOE=90°-θ,|
|=sinθ,求得
•
=
sin2θ,由此可得它的范围.
| OE |
| 1 |
| 2 |
| π |
| 2 |
| OD |
| OD |
| OE |
| 1 |
| 2 |
解答:
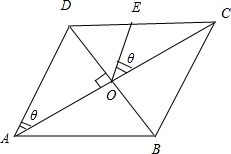 解:菱形ABCD,边长为1,E为CD的中点,O为两对角线交点,则|
解:菱形ABCD,边长为1,E为CD的中点,O为两对角线交点,则|
|=
.
设∠DAO=θ,则 θ∈(0
),∠DOE=90°-θ,|
|=|
|sinθ=sinθ,
则
•
=sinθ•
•cos(90°-θ )=
sin2θ∈(0,
),
故答案为:(0,
).
 解:菱形ABCD,边长为1,E为CD的中点,O为两对角线交点,则|
解:菱形ABCD,边长为1,E为CD的中点,O为两对角线交点,则|| OE |
| 1 |
| 2 |
设∠DAO=θ,则 θ∈(0
| π |
| 2 |
| OD |
| AD |
则
| OD |
| OE |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:(0,
| 1 |
| 2 |
点评:本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量的数量积的定义,属于基础题.

练习册系列答案
相关题目
先把函数f(x)=sin(x-
)的图象上各点的横坐标变为原来的
倍(纵坐标不变),再把新得到的图象向右平移
个单位,得到y=g(x)的图象.当x∈(
,
))时,函数g(x)的值域为( )
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 4 |
| 3π |
| 4 |
A、(-
| ||||||||
B、(-
| ||||||||
C、(-
| ||||||||
| D、[-1,0) |
若△ABC的内角A、B、C满足
=
=
,则cosB=( )
| 2 |
| sinA |
| 3 |
| sinB |
| 4 |
| sinC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知在等差数列{an}中,a3+a6+a10+a13=32,则a8=( )
| A、12 | B、8 | C、6 | D、4 |
设全集U=R,A={x|y=ln(1-x)},B={x||x-1|<1},则(∁UA)∩B=( )
| A、(-2,1) |
| B、(-2,1] |
| C、[1,2) |
| D、(1,2) |