题目内容
已知正项等差数列{an}的前n项和为Sn且满足a1+a5=
,S7=63.
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)若数列{bn}满足b1=a1且bn+1-bn=an+1,求数列{
}的前n项和Tn.
| 2 |
| 7 |
| a | 2 3 |
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)若数列{bn}满足b1=a1且bn+1-bn=an+1,求数列{
| 1 |
| bn |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)根据已知条件建立方程组,通过解方程求出首项和公差,进一步求出数列的通项公式.
(Ⅱ)首先利用叠加法求出数列的通项公式,进一步利用裂项相消法求数列的和.
(Ⅱ)首先利用叠加法求出数列的通项公式,进一步利用裂项相消法求数列的和.
解答:
解:(Ⅰ)法一:设正项等差数列{an}的首项为a1,公差为d,an>0
则
,
得
∴an=2n+1
法二:∵{an}是等差数列且a1+a5=
a32,∴2a3=
a32,
又∵an>0∴a3=7.…(2分)∵S7=
=7a4=63∴a4=9,
∴d=a4-a3=2,∴an=a3+(n-3)d=2n+1.
(Ⅱ)∵bn+1-bn=an+1且an=2n+1,
∴bn+1-bn=2n+3
当n≥2时,bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1
=(2n+1)+(2n-1)+…+5+3=n(n+2),
当n=1时,b1=3满足上式,bn=n(n+2)
∴
=
=
(
-
)
=
(1+
-
-
)=
-
(
+
).
则
|
得
|
∴an=2n+1
法二:∵{an}是等差数列且a1+a5=
| 2 |
| 7 |
| 2 |
| 7 |
又∵an>0∴a3=7.…(2分)∵S7=
| 7(a1+a7) |
| 2 |
∴d=a4-a3=2,∴an=a3+(n-3)d=2n+1.
(Ⅱ)∵bn+1-bn=an+1且an=2n+1,
∴bn+1-bn=2n+3
当n≥2时,bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1
=(2n+1)+(2n-1)+…+5+3=n(n+2),
当n=1时,b1=3满足上式,bn=n(n+2)
∴
| 1 |
| bn |
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
|
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
点评:本题考查的知识要点:数列的通项公式的求法,利用裂项相消法求数列的和,属于基础题型.

练习册系列答案
相关题目
先把函数f(x)=sin(x-
)的图象上各点的横坐标变为原来的
倍(纵坐标不变),再把新得到的图象向右平移
个单位,得到y=g(x)的图象.当x∈(
,
))时,函数g(x)的值域为( )
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 4 |
| 3π |
| 4 |
A、(-
| ||||||||
B、(-
| ||||||||
C、(-
| ||||||||
| D、[-1,0) |
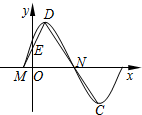 右图为函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<
右图为函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<
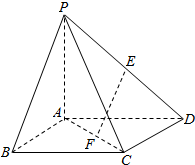 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E、F分别为PD、AC上的动点,且
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E、F分别为PD、AC上的动点,且