题目内容
已知l1,l2是分别经过A(2,1),B(0,2)两点的两条平行直线,当l1,l2之间的距离最大时,直线l1的方程是 .
考点:两条平行直线间的距离
专题:直线与圆
分析:l1,l2间的距离最大时,AB和这两条直线都垂直.由斜率公式求得AB的斜率,取负倒数可得直线l1的斜率,用点斜式求直线l1的方程.
解答:
解:由题意可得,l1,l2间的距离最大时,AB和这两条直线都垂直.
由于AB的斜率为
=-
,故直线l1的斜率为:2,故它的方程是 y-1=2(x-2),化简为 2x-y-3=0,
故答案为:2x-y-3=0.
由于AB的斜率为
| 1-2 |
| 2-0 |
| 1 |
| 2 |
故答案为:2x-y-3=0.
点评:本题主要考查直线的斜率公式,用点斜式求直线的方程,属于中档题.

练习册系列答案
相关题目
某中学有高中生4000人,其中高一1800人,高二1200人,高三1000人,为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为n的样本,已知从高二学生生中抽取90人,则n为( )
| A、300 | B、200 |
| C、150 | D、100 |
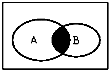 已知全集U为实数集,集合 A={x|x2-2x-3<0},B={x|y=ln(1-x)},则如图中阴影部分表示的集合为( )
已知全集U为实数集,集合 A={x|x2-2x-3<0},B={x|y=ln(1-x)},则如图中阴影部分表示的集合为( )| A、{x|x-1≤x<3} |
| B、{x|x<3} |
| C、{x|x≤-1} |
| D、{x|-1<x<1} |
将-300°化为弧度为( )
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|