题目内容
P是
-
=1（a＞0，b＞0）的左支上的一点，F1，F2分别为左、右焦点，且焦距为2c，△PF1F2的内切圆的圆心的横坐标为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、-a | B、-b |
| C、-c | D、a+b-c |
考点：双曲线的简单性质
专题：计算题,直线与圆,圆锥曲线的定义、性质与方程
分析：充分利用平面几何图形的性质解题．因从同一点出发的切线长相等，得PM|=|PN|，|F1M|=|F1D|，|F2N|=|F2D|，再结合双曲线的定义得|F1D|-|F2D|=-2a，从而即可求得△PF1F2的内心的横坐标．
解答：
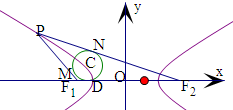解：记△PF1F2的内切圆圆心为C，
边PF1、PF2、F1F2上的切点分别为M、N、D，
易见C、D横坐标相等，
|PM|=|PN|，|F1M|=|F1D|，|F2N|=|F2D|，
由|PF2|-|PF1|=2a，
即：|PM|+|MF1|-（|PN|+|NF2|）=-2a，
得|MF1|-|NF2|=-2a即|F1D|-|F2D|=-2a，
记C的横坐标为x0，则D（x0，0），
于是：x0+c-（c-x0）=-2a，
得x0=-a，
则内切圆的圆心的横坐标为-a．
故选A．
解：记△PF1F2的内切圆圆心为C，边PF1、PF2、F1F2上的切点分别为M、N、D，
易见C、D横坐标相等，
|PM|=|PN|，|F1M|=|F1D|，|F2N|=|F2D|，
由|PF2|-|PF1|=2a，
即：|PM|+|MF1|-（|PN|+|NF2|）=-2a，
得|MF1|-|NF2|=-2a即|F1D|-|F2D|=-2a，
记C的横坐标为x0，则D（x0，0），
于是：x0+c-（c-x0）=-2a，
得x0=-a，
则内切圆的圆心的横坐标为-a．
故选A．
点评：本题主要考查了双曲线的定义、双曲线的应用及转化问题的能力，属于中档题．
练习册系列答案
相关题目
已知A，B，C表示三个不同的点，l表示直线，α，β表示平面，则下列推断错误的是（ ）
| A、A∈l，B∈l，A∈α，B∈α⇒l?α |
| B、A∈α，B∈α，C∈α，A∈β，B∈β，C∉β⇒α∩β=直线AB |
| C、l?α，A∈l⇒A∉α |
| D、A，B，C∈α，A，B，C∈β，A，B，C不共线⇒α，β重合 |
已知{an}是等差数列，Sn为其前n项和，n∈N，若a8=-3，S20=30，则a13的值为（ ）
| A、-8 | B、-6 | C、6 | D、12 |
