题目内容
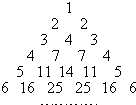
用部分自然数构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aii=i,每行中的其他各数分别等于其“肩膀”上的两个数之和.设第n(n为N+)行的第二个数为bn(n≥2),
(1)写出第6行的第三个数;
(2)写出bn+1与bn的关系并求bn(n≥2);
(3)设(bn-1)cn=1(n≥2),求证:1≤c2+c3+…+cn<2.
(1)写出第6行的第三个数;
(2)写出bn+1与bn的关系并求bn(n≥2);
(3)设(bn-1)cn=1(n≥2),求证:1≤c2+c3+…+cn<2.

考点:进行简单的合情推理
专题:等差数列与等比数列,推理和证明
分析:(1)根据已知中图象,可得第6行的第三个数.
(2)根据ai1=aii=i,每行中的其他各数分别等于其“肩膀”上的两个数之和.可得bn+1=bn+n,利用.
(3)由(2)可得cn=
=2(
-
),结合裂项相消法,可得答案.
(2)根据ai1=aii=i,每行中的其他各数分别等于其“肩膀”上的两个数之和.可得bn+1=bn+n,利用.
(3)由(2)可得cn=
| 2 |
| n(n-1) |
| 1 |
| n-1 |
| 1 |
| n |
解答:
解:(1)由已知中的图象可得:
第6行的第三个数为25;
(2)由已知得bn+1=bn+n,
∴bn+1-bn=n,
∴bn-bn-1=n-1,
bn-1-bn-2=n-2,
…,
b3-b2=2,
b2-b1=1,
累加得:
bn-b1=n-1+n-2+…+2+1=
,
又∵b1=1,
∴bn=
+1
证明:(3)∵(bn-1)cn=1,即
cn=1,
∴cn=
=2(
-
),
∴c2+c3+…+cn=2(1-
+
-
+…+
-
)=2(1-
),
∵n≥2,
∴0<
≤
,
∴1≤c2+c3+…+cn<2.
第6行的第三个数为25;
(2)由已知得bn+1=bn+n,
∴bn+1-bn=n,
∴bn-bn-1=n-1,
bn-1-bn-2=n-2,
…,
b3-b2=2,
b2-b1=1,
累加得:
bn-b1=n-1+n-2+…+2+1=
| n(n-1) |
| 2 |
又∵b1=1,
∴bn=
| n(n-1) |
| 2 |
证明:(3)∵(bn-1)cn=1,即
| n(n-1) |
| 2 |
∴cn=
| 2 |
| n(n-1) |
| 1 |
| n-1 |
| 1 |
| n |
∴c2+c3+…+cn=2(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| n |
∵n≥2,
∴0<
| 1 |
| n |
| 1 |
| 2 |
∴1≤c2+c3+…+cn<2.
点评:本题考查的知识点是归纳推理,裂项相消法求和,是数列的推理和证明的综合应用,难度不大,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=
+xlnx,则曲线y=f(x)在x=1处的切线方程为( )
| 2 |
| x |
| A、x-y-3=0 |
| B、x-y+3=0 |
| C、x+y-3=0 |
| D、x+y+3=0 |
P是
-
=1(a>0,b>0)的左支上的一点,F1,F2分别为左、右焦点,且焦距为2c,△PF1F2的内切圆的圆心的横坐标为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、-a | B、-b |
| C、-c | D、a+b-c |
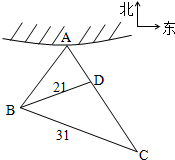 如图所示,近日我渔船编队在岛A周围海域作业,在岛A的南偏西20°方向有一个海面观测站B,某时刻观测站发现有不明船只向我渔船编队靠近,现测得与B相距31海里的C处有一艘海警船巡航,上级指示海警船沿北偏西40°方向,以40海里/小时的速度向岛A直线航行以保护我渔船编队,30分钟后到达D处,此时观测站测得B,D间的距离为21海里.
如图所示,近日我渔船编队在岛A周围海域作业,在岛A的南偏西20°方向有一个海面观测站B,某时刻观测站发现有不明船只向我渔船编队靠近,现测得与B相距31海里的C处有一艘海警船巡航,上级指示海警船沿北偏西40°方向,以40海里/小时的速度向岛A直线航行以保护我渔船编队,30分钟后到达D处,此时观测站测得B,D间的距离为21海里.