题目内容
如图，已知长方体ABCD-A1B1C1D1的对角线A1C与侧棱BB1所成的角为45°，且AB=BC=1，求A1C与侧面BB1C1C所成角的大小．考点：直线与平面所成的角
专题：空间角
分析：连结AC，B1C，由已知得∠AA1C=45°，AA1=AC=
=
，∠A1CB1是直线A1C与平面BB1C1C所成角，
由此能求出A1C与侧面BB1C1C所成角的大小．
| AB2+BC2 |
| 2 |
由此能求出A1C与侧面BB1C1C所成角的大小．
解答：
解：
连结AC，B1C，
∵长方体ABCD-A1B1C1D1的对角线A1C与侧棱BB1所成的角为45°，且AB=BC=1，
∴∠AA1C=45°，∴AA1=AC=
=
，
∵A1B1⊥平面BCC1B1，∴∠A1CB1是直线A1C与平面BB1C1C所成角，
∵A1B1=1，B1C=
=
，
∴tan∠A1CB1=
=
=
，
∴∠A1CB1=30°．
∴A1C与侧面BB1C1C所成角的大小为30°．
连结AC，B1C，∵长方体ABCD-A1B1C1D1的对角线A1C与侧棱BB1所成的角为45°，且AB=BC=1，
∴∠AA1C=45°，∴AA1=AC=
| AB2+BC2 |
| 2 |
∵A1B1⊥平面BCC1B1，∴∠A1CB1是直线A1C与平面BB1C1C所成角，
∵A1B1=1，B1C=
| BC2+BB12 |
| 3 |
∴tan∠A1CB1=
| A1B1 |
| B1C |
| 1 | ||
|
| ||
| 3 |
∴∠A1CB1=30°．
∴A1C与侧面BB1C1C所成角的大小为30°．
点评：本题考查线面平行，线面垂直的性质的应用，考查直线与平面所成角的求法，解题时要注意空间中线线、线面、面面间的位置关系及性质的合理运用，是中档题．
练习册系列答案
阅读快车系列答案
相关题目
设a=log23.9，b=log20.7，c=2，则（ ）
| A、b＜a＜c |
| B、a＜b＜c |
| C、c＜a＜b |
| D、c＜b＜a |
已知在△ABC中，D是AB边上的一点，
=λ（
+
），|
|=2，|
|=1，若
=
，
=
，则用
，
表示
为（ ）
| CD |
| ||
|
|
| ||
|
|
| CA |
| CB |
| CA |
| b |
| CB |
| a |
| a |
| b |
| CD |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
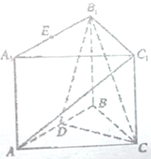如图，在直三棱柱ABC-A1B1C1中，∠ABC=90°，AB=BC=AA1=2，D是AB的中点．