题目内容
曲线y=sin(
-x)在点A(-
,
)处的切线方程为 .
| π |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:运用诱导公式,求出函数的导数,求得切线的斜率,由点斜式方程即可得到所求切线方程.
解答:
解:y=sin(
-x)即为y=cosx,
则导数y′=-sinx,
即有在点A(-
,
)处的切线斜率为-sin(-
)=
,
则在点A(-
,
)处的切线方程为y-
=
(x+
),
即为3x-2
y+π+
=0.
故答案为:3x-2
y+π+
=0.
| π |
| 2 |
则导数y′=-sinx,
即有在点A(-
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| ||
| 2 |
则在点A(-
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
即为3x-2
| 3 |
| 3 |
故答案为:3x-2
| 3 |
| 3 |
点评:本题考查导数的几何意义:函数在某点处的导数即为曲线在该点处的导数,同时考查诱导公式,正确求导和运用点斜式方程是解题的关键,属于基础题.

练习册系列答案
相关题目
“x>1”是“ln(ex+1)>1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、非充分非必要条件 |
已知
与
为不共线的单位向量,其夹角θ,设
=λ
+
,
=
+μ
,有下列四个命题:
p1:|
+
|>|
-
|?θ∈(0,
);p2:|
+
|>|
-
|?θ∈(
,π);
p3:若A,B,C共线?λ+μ=1;p4:若A,B,C共线?λ•μ=1.其中真命题的是( )
| a |
| b |
| AB |
| a |
| b |
| AC |
| a |
| b |
p1:|
| a |
| b |
| a |
| b |
| π |
| 2 |
| a |
| b |
| a |
| b |
| π |
| 2 |
p3:若A,B,C共线?λ+μ=1;p4:若A,B,C共线?λ•μ=1.其中真命题的是( )
| A、p1,p4 |
| B、p1,p3 |
| C、p2,p3 |
| D、p2,p4 |
已知D为△ABC的边BC的中点,△ABC所在平面内有一个点P,满足
=
+
,则
的值为( )
| PA |
| PB |
| PC |
|
| ||
|
|
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
 如图,已知长方体ABCD-A1B1C1D1的对角线A1C与侧棱BB1所成的角为45°,且AB=BC=1,求A1C与侧面BB1C1C所成角的大小.
如图,已知长方体ABCD-A1B1C1D1的对角线A1C与侧棱BB1所成的角为45°,且AB=BC=1,求A1C与侧面BB1C1C所成角的大小.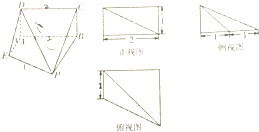 已知一个空间几何体的直观图和三视图(尺寸如图所示)
已知一个空间几何体的直观图和三视图(尺寸如图所示)