题目内容
7.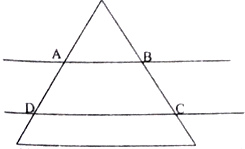 将边长为4正三角形薄片,用平行于底边的两条直线剪成三块(如图所示),这两条平行线间的距离为$\sqrt{3}$,其中间一块是梯形记为ABCD,记$S=\frac{{{{({梯形ABCD的周长})}^2}}}{梯形ABCD的面积}$,则S的最小值为$\frac{32\sqrt{3}}{3}$.
将边长为4正三角形薄片,用平行于底边的两条直线剪成三块(如图所示),这两条平行线间的距离为$\sqrt{3}$,其中间一块是梯形记为ABCD,记$S=\frac{{{{({梯形ABCD的周长})}^2}}}{梯形ABCD的面积}$,则S的最小值为$\frac{32\sqrt{3}}{3}$.
分析 作AE⊥CD于E,作BF⊥CD于F,设AB=x,用x表示出梯形的周长和面积,求出S关于x的函数,利用基本不等式得出S的最小值.
解答  解:作AE⊥CD于E,作BF⊥CD于F,则AE=BF=$\sqrt{3}$,
解:作AE⊥CD于E,作BF⊥CD于F,则AE=BF=$\sqrt{3}$,
∵∠ADE=∠BCF=60°,
∴DE=CF=1,AD=BC=2,
设AB=x(0≤x≤4),则梯形ABCD的周长为2x+6,
梯形ABCD的面积为$\frac{\sqrt{3}}{2}$(x+x+2)=$\sqrt{3}$(x+1).
∴S=$\frac{(2x+6)^{2}}{\sqrt{3}(x+1)}$=$\frac{4}{\sqrt{3}}$•$\frac{{x}^{2}+6x+9}{x+1}$=$\frac{4}{\sqrt{3}}$•(x+1+$\frac{4}{x+1}$+4)≥$\frac{4}{\sqrt{3}}•(4+4)$=$\frac{32\sqrt{3}}{3}$.
当且仅当x+1=$\frac{4}{x+1}$即x=2时取等号.
故答案为:$\frac{{32\sqrt{3}}}{3}$.
点评 本题考查了函数解析式的求解,基本不等式与函数最值的计算,属于中档题.

练习册系列答案
相关题目
15.某公司在一次对员工的休闲方式(看电视与运动)与性别之间是否有关系的调查中,共调查了124人,其中女性70人中主要休闲方式是看电视的有43人,男性中主要休闲方式是运动的有33人.
(1)根据以上数据建立一个2×2的列联表;
(2)检验性别与休闲方式是否有关系.
${Χ^2}=\frac{{n{{({n_{11}}{n_{22}}-{n_{12}}{n_{21}})}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$
(1)根据以上数据建立一个2×2的列联表;
(2)检验性别与休闲方式是否有关系.
${Χ^2}=\frac{{n{{({n_{11}}{n_{22}}-{n_{12}}{n_{21}})}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$
| P(Χ2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
2.设函数f(x)=sin(2x+φ)+cos(2x+φ)(|φ|<$\frac{π}{2}$)为偶函数,则φ=( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
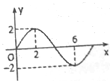 函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+…+f(2017)=$\sqrt{2}$.
函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+…+f(2017)=$\sqrt{2}$.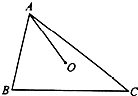 如图,在△ABC中,AB=5,AC=9,若O为△ABC内一点,且满足|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|,则$\overrightarrow{AO}$•$\overrightarrow{BC}$的值是28.
如图,在△ABC中,AB=5,AC=9,若O为△ABC内一点,且满足|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|,则$\overrightarrow{AO}$•$\overrightarrow{BC}$的值是28.